-
Home
- Principles of digital communications
- Chapter 1: signals and systems
- Introduction to stochastic
Definitions, distributions, and stationarity
Stochastic Process
- Given a sample space, a stochastic process is an indexed collection
of random variables defined for each
.
Received signal at an antenna as in
[link] .

For a given
,
is a random variable with a distribution
First-order distribution
First-order stationary process
- If
is not a function of time then
is called a first-order stationary process.
Second-order distribution
for all
,
,
,
Nth-order distribution
th-order stationary : A
random process is stationary of order
if
Strictly stationary : A process is strictly stationary if it
is
th order stationary for all
.
where
is the deterministic carrier frequency and
is a random variable defined over
and is assumed to be a uniform random variable;
i.e. ,
This process is stationary of order 1.
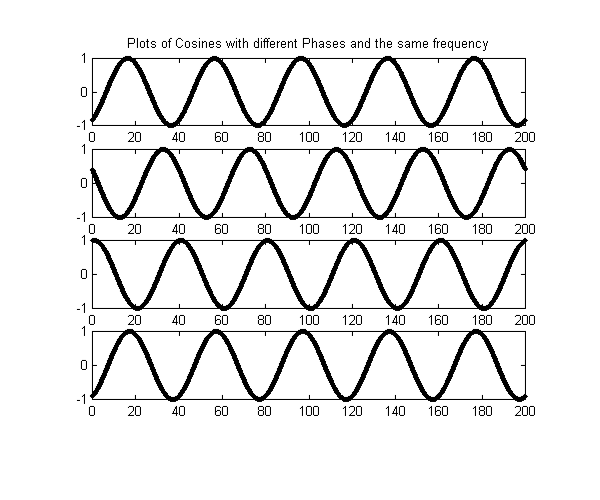
The second order stationarity can be determined by first considering
conditional densities and the joint density. Recall that
Then the relevant step is to find
Note that

Note that this is only a function of
.
Every
seconds, a fair coin
is tossed. If heads, then
for
.If tails, then
for
.
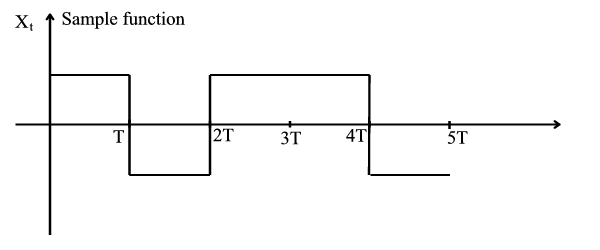
for all
.
is stationary of order 1.
Second order probability mass function
The conditional pmf
when
and
for some
.
for all
and for all
when
and
with
Source:
OpenStax, Principles of digital communications. OpenStax CNX. Jul 29, 2009 Download for free at http://cnx.org/content/col10805/1.1
Google Play and the Google Play logo are trademarks of Google Inc.




