| << Chapter < Page | Chapter >> Page > |
The focus of this course is on digital communication, which involves transmission of information, in its most general sense,from source to destination using digital technology. Engineering such a system requires modeling both the informationand the transmission media. Interestingly, modeling both digital or analog information and many physical media requires aprobabilistic setting. In this chapter and in the next one we will review the theory of probability, model random signals, andcharacterize their behavior as they traverse through deterministic systems disturbed by noise and interference. Inorder to develop practical models for random phenomena we start with carrying out a random experiment. We then introducedefinitions, rules, and axioms for modeling within the context of the experiment. The outcome of a random experiment isdenoted by . The sample space is the set of all possible outcomes of a random experiment. Such outcomescould be an abstract description in words. A scientific experiment should indeed be repeatable where each outcome couldnaturally have an associated probability of occurrence. This is defined formally as the ratio of the number of times the outcomeoccurs to the total number of times the experiment is repeated.
A random variable is the assignment of a real number to each outcome of a random experiment.
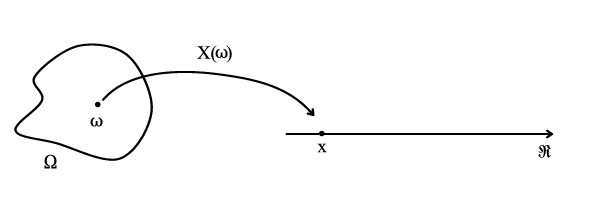
Roll a dice. Outcomes
= dots on the face of the dice.
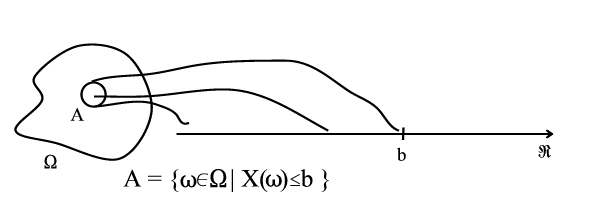
Probability assignments on intervals
Two random variables defined on an experiment have joint distribution
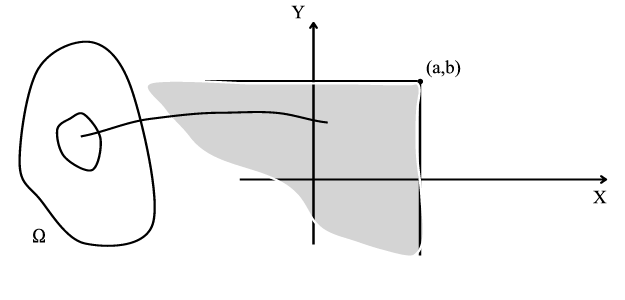
Joint pdf can be obtained if they are jointly continuous
Joint pmf if they are jointly discrete
Conditional density function
Two random variables are independent if
Statistical quantities to represent some of the characteristics of a random variable.

Notification Switch
Would you like to follow the 'Principles of digital communications' conversation and receive update notifications?