| << Chapter < Page | Chapter >> Page > |
Let’s now use this formula to calculate the surface area of each of the bands formed by revolving the line segments around the A representative band is shown in the following figure.
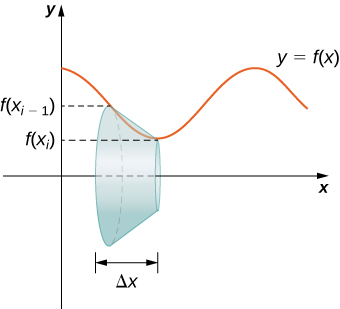
Note that the slant height of this frustum is just the length of the line segment used to generate it. So, applying the surface area formula, we have
Now, as we did in the development of the arc length formula, we apply the Mean Value Theorem to select such that This gives us
Furthermore, since is continuous, by the Intermediate Value Theorem, there is a point such that so we get
Then the approximate surface area of the whole surface of revolution is given by
This almost looks like a Riemann sum, except we have functions evaluated at two different points, and over the interval Although we do not examine the details here, it turns out that because is smooth, if we let the limit works the same as a Riemann sum even with the two different evaluation points. This makes sense intuitively. Both and are in the interval so it makes sense that as both and approach Those of you who are interested in the details should consult an advanced calculus text.
Taking the limit as we get
As with arc length, we can conduct a similar development for functions of to get a formula for the surface area of surfaces of revolution about the These findings are summarized in the following theorem.
Let be a nonnegative smooth function over the interval Then, the surface area of the surface of revolution formed by revolving the graph of around the x -axis is given by
Similarly, let be a nonnegative smooth function over the interval Then, the surface area of the surface of revolution formed by revolving the graph of around the is given by
Let over the interval Find the surface area of the surface generated by revolving the graph of around the Round the answer to three decimal places.
The graph of and the surface of rotation are shown in the following figure.
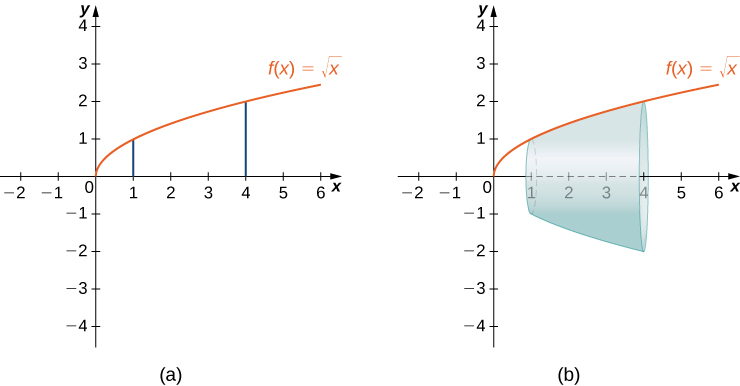
We have Then, and Then,
Let Then, When and when This gives us
Let over the interval Find the surface area of the surface generated by revolving the graph of around the Round the answer to three decimal places.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?