| << Chapter < Page | Chapter >> Page > |
Let Consider the portion of the curve where Find the surface area of the surface generated by revolving the graph of around the
Notice that we are revolving the curve around the and the interval is in terms of so we want to rewrite the function as a function of y . We get The graph of and the surface of rotation are shown in the following figure.
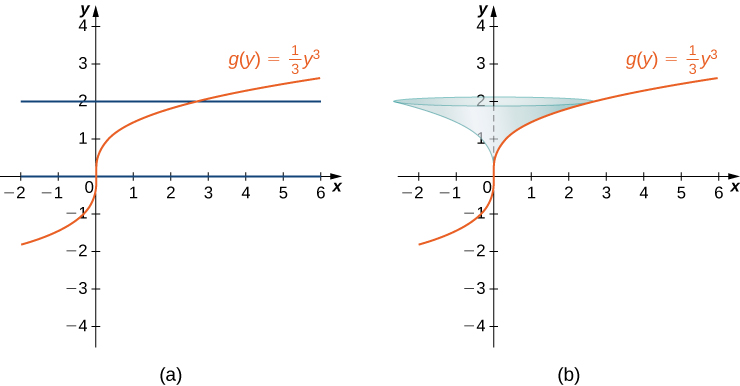
We have so and Then
Let Then When and when Then
Let over the interval Find the surface area of the surface generated by revolving the graph of around the
For the following exercises, find the length of the functions over the given interval.
Pick an arbitrary linear function over any interval of your choice Determine the length of the function and then prove the length is correct by using geometry.
Find the surface area of the volume generated when the curve revolves around the from to as seen here.
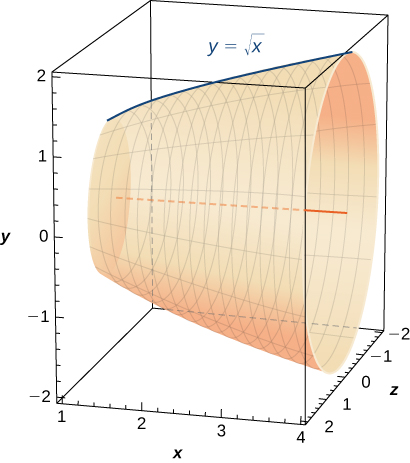
Find the surface area of the volume generated when the curve revolves around the from to

For the following exercises, find the lengths of the functions of over the given interval. If you cannot evaluate the integral exactly, use technology to approximate it.
For the following exercises, find the lengths of the functions of over the given interval. If you cannot evaluate the integral exactly, use technology to approximate it.
[T] from to
[T] from to
[T] on to
For the following exercises, find the surface area of the volume generated when the following curves revolve around the If you cannot evaluate the integral exactly, use your calculator to approximate it.
For the following exercises, find the surface area of the volume generated when the following curves revolve around the If you cannot evaluate the integral exactly, use your calculator to approximate it.
[T] from to
[T] from to
[T] from to
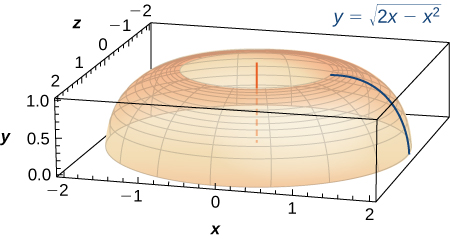
The base of a lamp is constructed by revolving a quarter circle around the from to as seen here. Create an integral for the surface area of this curve and compute it.
A light bulb is a sphere with radius in. with the bottom sliced off to fit exactly onto a cylinder of radius in. and length in., as seen here. The sphere is cut off at the bottom to fit exactly onto the cylinder, so the radius of the cut is in. Find the surface area (not including the top or bottom of the cylinder).

[T] A lampshade is constructed by rotating around the from to as seen here. Determine how much material you would need to construct this lampshade—that is, the surface area—accurate to four decimal places.

[T] An anchor drags behind a boat according to the function where represents the depth beneath the boat and is the horizontal distance of the anchor from the back of the boat. If the anchor is ft below the boat, how much rope do you have to pull to reach the anchor? Round your answer to three decimal places.
[T] You are building a bridge that will span ft. You intend to add decorative rope in the shape of where is the distance in feet from one end of the bridge. Find out how much rope you need to buy, rounded to the nearest foot.
ft
For the following exercises, find the exact arc length for the following problems over the given interval.
from to ( Hint: Recall trigonometric identities.)
Draw graphs of and For as increases, formulate a prediction on the arc length from to Now, compute the lengths of these three functions and determine whether your prediction is correct.
Compare the lengths of the parabola and the line from as increases. What do you notice?
Solve for the length of from Show that from to is twice as long. Graph both functions and explain why this is so.
Answers may vary
[T] Which is longer between and the hyperbola or the graph of
Explain why the surface area is infinite when is rotated around the for but the volume is finite.
For more information, look up Gabriel’s Horn.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?