| << Chapter < Page | Chapter >> Page > |
Motion of a balloon
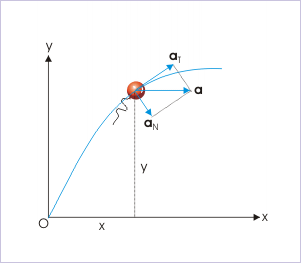
Thus, we see that total acceleration is not only one dimensional, but constant as well. However, this does not mean that component accelerations viz tangential and normal accelerations are also constant. We need to investigate their expressions. We can obtain tangential acceleration as time rate of change of the magnitude of velocity i.e. the time rate of change of speed. We, therefore, need to first know an expression of the speed. Now, speed is :
Differentiating with respect to time, we have :
In order to find the normal acceleration, we use the fact that total acceleration is vector sum of two mutually perpendicular tangential and normal accelerations.
Problem : The coordinates of a particle moving in a plane are given by x = A cos(ωt) and y = B sin (ωt) where A, B (<A) and “ω” are positive constants of appropriate dimensions. Prove that the velocity and acceleration of the particle are normal to each other at t = π/2ω.
Solution : By differentiation, the components of velocity and acceleration are as given under :
The components of velocity in “x” and “y” directions are :
The components of acceleration in “x” and “y” directions are :
At time, and . Putting this value in the component expressions, we have :
Motion along elliptical path
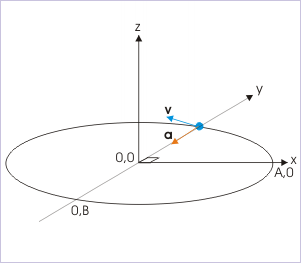
The net velocity is in negative x-direction, whereas net acceleration is in negative y-direction. Hence at , velocity and acceleration of the particle are normal to each other.
Problem : Position vector of a particle is :
Show that velocity vector is perpendicular to position vector.
Solution : We shall use a different technique to prove as required. We shall use the fact that scalar (dot) product of two perpendicular vectors is zero. We, therefore, need to find the expression of velocity. We can obtain the same by differentiating the expression of position vector with respect to time as :
To check whether velocity is perpendicular to the position vector, we take the scalar product of r and v as :
This means that the angle between position vector and velocity are at right angle to each other. Hence, velocity is perpendicular to position vector.
Problem : The coordinates of a particle moving in a plane are given by x = A cos(ω t) and y = B sin (ω t) where A, B (<A) and ω are positive constants of appropriate dimensions. Find the displacement of the particle in time interval t = 0 to t = π/2 ω.
Solution : In order to find the displacement, we shall first know the positions of the particle at the start of motion and at the given time. Now, the position of the particle is given by coordinates :
and
At t = 0, the position of the particle is given by :
At , the position of the particle is given by :
Motion along an elliptical path
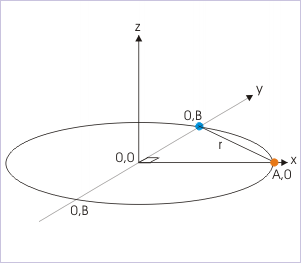
Therefore , the displacement in the given time interval is :

Notification Switch
Would you like to follow the 'Kinematics fundamentals' conversation and receive update notifications?