| << Chapter < Page | Chapter >> Page > |
Evaluate each of the following.
a. b. c. d.
To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN-1, ARCSIN, or ASIN.
In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.
In these examples and exercises, the answers will be interpreted as angles and we will use as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.
Evaluate using a calculator.
Because the output of the inverse function is an angle, the calculator will give us a degree value if in degree mode and a radian value if in radian mode. Calculators also use the same domain restrictions on the angles as we are using.
In radian mode, In degree mode, Note that in calculus and beyond we will use radians in almost all cases.
Evaluate using a calculator.
1.9823 or 113.578°
Given two sides of a right triangle like the one shown in [link] , find an angle.
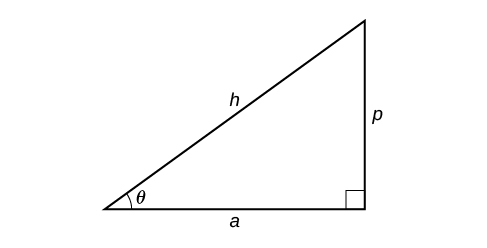
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.
Solve the triangle in [link] for the angle
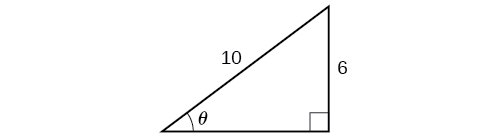
radians
There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let and be two different trigonometric functions belonging to the set and let and be their inverses.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?