2.2 Vorm en ruimte  (Page 3/3)

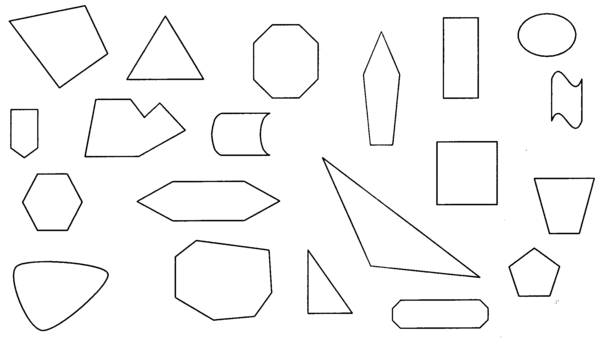
Hier is ‘n klompie geslote plat figure; kleur hulle in, en skryf die naam van elk op die vorm.

B. Ondersoek

Kies vier veelhoeke uit die boonste oefening; almal reëlmatig, maar met verskillende aantal sye. Meet nou die binnehoeke van elk. Probeer uitvind of daar dalk ‘n formule bepaal kan word wat kan voorspel hoe groot die hoeke is, en wat die som van die hoeke sal wees.

Die volgende tabel sal help. Soos jy kan aflei, is daar oneindig veel poligone.

• Die eienskappe in die tabel is baie handig wanneer daar besluit moet word hoe om ‘n vloer te teël met reëlmatige veelhoeke sodat hulle nie oorvleuel of gate laat nie. Party veelhoeke sal met ander gekombineer kan word, ander sal alleen werk.
• Ontwerp en teken jou eie herhalende teëlpatroon deur slegs reëlmatige veelhoeke te gebruik, en kleur dit so in dat die patroon duidelik is.

C. Driedimensionele geslote figure .

• As hierdie figure se sye uit veelhoeke bestaan, noem ons hulle polihedra of veelvlakke . ‘n Reëlmatige polihedron (veelvlak) se kante is kongruente reëlmatige poligone, met binnehoeke dieselfde vorm en grootte.
• Anders as die veelhoeke, bestaan daar net vyf reëlmatige veelvlakke. Hulle is al bekend sedert die dae van Plato en die Griekse wiskundiges; daarom staan hulle bekend as die vyf Platoniese ruimtefigure.

D. Projek

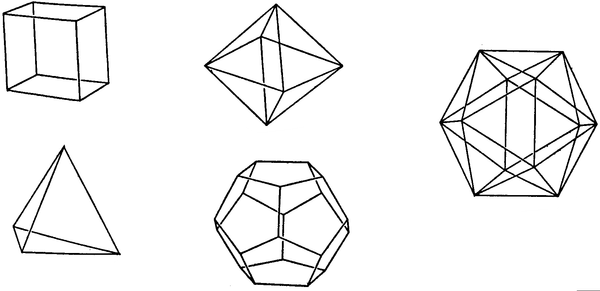
Vors die vyf Platoniese ruimtefigure na om hulle name en eienskappe op te spoor, asook ander interessante feite en verhale oor hulle. Maak ‘n aantreklike plakkaat of modelle van die figure wat die feite van elk aantoon. Hieronder is diagramme van die figure.

Assessering

Memorandum

Bespreking

• Ingesluit by hierdie gids is daar twee blads y e figure vir die konstruksie van eenvoudige regte prismas. Dupliseer genoeg vir die leerders om ten minste twee elk van die figure te maak. Probeer om hiervoor ligte karton of swaar papier te gebruik. Leerders kan gevra word om dele (soos onder-en bokant) in te kleur om die begrip van die moeilike formules duideliker te maak.

• In die algemeen is die twee formules vir regte prismas:
• Totale Buite Oppervlakte = tweemaal die basis–area + prisma–hoogte × basis–omtrek
• Volume = basis – area × prisma – hoogte
• Die toepaslike eenhede (tot die mag 2 of 3) vir elke formule moet altyd vereis word.
• Daar is nog ‘n moontlike probleem omdat die woord hoogte gebruik word by die berekening van oppervlaktes van driehoeke asook by die mate van ‘n prisma. Gebruik gerus h by die driehoek, en H by die prisma.
• As leerders verwar word deur die komponente van die formules, is die metode waar die stappe opgebreek word, van veel hulp. Natuurlik sal die bedrewe leerder direk reg in die formule kan instel. Dis ‘n effektiese gebruik en kan gerus aangemoedig word.

Oefening: Oplossings:

Reghoekige prisma: TBO = 412 cm ² Vol = 480 cm ³

Driehoekige prisma: TBO = 307,71 cm ² Vol = 360 cm ³

Silinder: TBO = 402,12 cm ² Vol = 603,19 cm ³

Ouma se Konfyt: Kastrol: Vol = 8 595,40 cm ²

11 Vierkantige bottels: Vol = 8 096 cm ²

11 Reghoekige bottels: Vol =8 633,63 cm ²

As ouma al die konfyt wil inkry moet sy die reghoekige botteltjies gebruik!

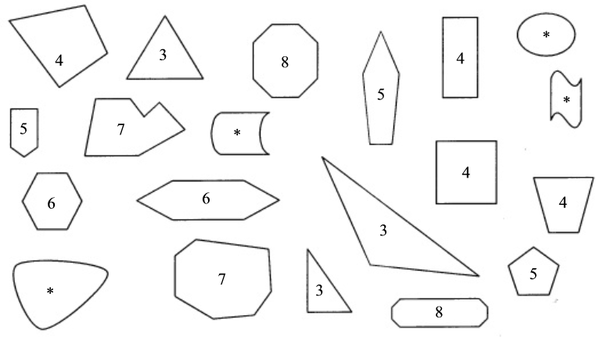
3 = driehoek; 4 = vierhoek; 5 = vyfhoek; 6 = seshoek; 7 = sewehoek; 8 = agthoek; * = nie veelhoek

Die

TOETS 1

1. Verduidelik hoe om ‘n regte prisma te herken.

2. Verduidelik hoe om die basis van ‘n regte prisma te bepaal.

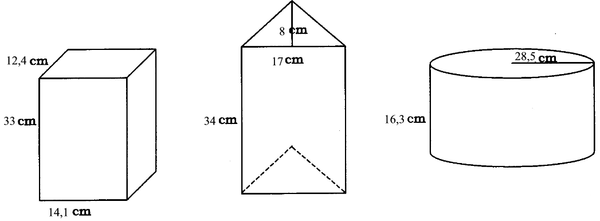
3. Bereken die totale buiteoppervlakte en volume van elk van die volgende drie prismas. Gee jou antwoord akkuraat tot twee desimale plekke.

Memorandum

1. Belangrike punte in verduideliking: driedimensioneel; bokant en onderkant kongruente plat- vlakke; sye reghoekig tot basis.

2. Enige redelike verduideliking, bv. as die gekose basis onder is, pas dit die beskrywing van ‘n regte prisma.

3. Reghoekige regte prisma: TBO = 1 939,68 cm ² Volume = 5 769,72 cm ³

Driehoekige regte prisma: TBO = 1 507,74 mm ² Volume = 2 312 mm ³

Silinder: TBO = 8 022,37 m ² Volume = 41 593,67 m ³