12.5 Hyperbolas  (Page 2/2)

Similarities between hyperbolas and ellipses

• The formula is identical, except for the replacement of $\mathrm{a+}$ with $\mathrm{a-}$ .
• The definition of $a$ is very similar. In a horizontal ellipse, you move horizontally $a$ from the center to the edges of the ellipse. (This defines the major axis.) In a horizontal hyperbola, you move horizontally $a$ from the center to the vertices of the hyperbola. (This defines the transverse axis.)
• $b$ defines a different, perpendicular axis.
• The definition of $c$ is identical: the distance from center to focus.

Differences between hyperbolas and ellipses

• The biggest difference is that for an ellipse, $a$ is always the biggest of the three variables; for a hyperbola, $c$ is always the biggest. This should be evident from looking at the drawings (the foci are inside an ellipse, outside a hyperbola). However, this difference leads to several other key distinctions.
• For ellipses, $a^2=b^2+c^2$ . For hyperbolas, $c^2=a^2+b^2$ .
• For ellipses, you tell whether it is horizontal or vertical by looking at which denominator is greater, since $a$ must always be bigger than $b$ . For hyperbolas, you tell whether it is horizontal or vertical by looking at which variable has a positive sign, the $x^2$ or the $y^2$ . The relative sizes of $a$ and $b$ do not distinguish horizontal from vertical.

In the example below, note that the process of getting the equation in standard form is identical with hyperbolas and ellipses. The extra last step—rewriting a multiplication by 4 as a division by $\frac{1}{4}$ —can come up with ellipses as easily as with hyperbolas. However, it did not come up in the last example, so it is worth taking note of here.

However, the process of graphing a hyperbola is quite different from the process of graphing an ellipse. Even here, however, some similarities lurk beneath the surface.

Graphing a hyperbola in standard form

Graph $(x-3{)}^2–\frac{(y+1{)}^2}{\frac{1}{4}}=1$	The problem, carried over from the example above, now in standard form.
Center: (3,–1)	Comes straight out of the equation, both signs changed, just as with circles and ellipses.
$a=1$ $b=\frac{1}{2}$	The square roots of the denominators, just as with the ellipse. But how do we tell which is which? In the case of a hyperbola, the $a$ always goes with the positive term . In this case, the $x^2$ term is positive, so the term under it is $a^2$ .
Horizontal hyperbola	Again, this is because the $x^2$ term is positive. If the $y^2$ were the positive term, the hyperbola would be vertical, and the number under the $y^2$ term would be considered $a^2$ .
$c=\sqrt{1^2+(\frac{1}{2}{)}^2}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2}$	Remember that the relationship is different: for hyperbolas, $c^2=a^2+b^2$
	Now we begin drawing. Begin by drawing the center at (3,–1). Now, since this is a horizontal ellipse, the vertices will be aligned horizontally around the center. Since $a=1$ , move 1 to the left and 1 to the right, and draw the vertices there.
	In the other direction—vertical, in this case—we have something called the “conjugate axis.” Move up and down by $b$ ( $\frac{1}{2}$ in this case) to draw the endpoints of the conjugate axis. Although not part of the hyperbola, they will help us draw it.
	Draw a box that goes through the vertices and the endpoints of the conjugate axis. The box is drawn in dotted lines to show that it is not the hyperbola.
	Draw diagonal lines through the corners of the box—also dotted, because they are also not the hyperbola.These lines are called the asymptotes , and they will guide you in drawing the hyperbola. The further it gets from the vertices, the closer the hyperbola gets to the asymptotes. However, it never crosses them.
	Now, at last, we are ready to draw the hyperbola. Beginning at the vertices, approach—but do not cross!—the asymptotes. So you see that the asymptotes guide us in setting the width of the hyperbola, performing a similar function to the latus rectum in parabolas.

Got questions? Get instant answers now!

The hyperbola is the most complicated shape we deal with in this course, with a lot of steps to memorize.

But there is also a very important concept hidden in all that, and that is the concept of an asymptote. Many functions have asymptotes, which you will explore in far greater depth in more advanced courses. An asymptote is a line that a function approaches, but never quite reaches. The asymptotes are the easiest way to confirm that a hyperbola is not actually two back-to-back parabolas. Although one side of a hyperbola resembles a parabola superficially, parabolas do not have asymptotic behavior—the shape is different.

Remember our comet? It flew into the solar system at a high speed, whipped around the sun, and flew away in a hyperbolic orbit. As the comet gets farther away, the sun’s influence becomes less important, and the comet gets closer to its “natural” path—a straight line. In fact, that straight line is the asymptote of the hyperbolic path.

Before we leave hyperbolas, I want to briefly mention a much simpler equation: $y=\frac{1}{x}$ . This is the equation of a diagonal hyperbola. The asymptotes are the $x$ and $y$ axes.

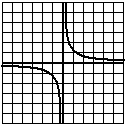
Although the equation looks completely different, the shape is identical to the hyperbolas we have been studying, except that it is rotated 45°.