| << Chapter < Page | Chapter >> Page > |
| 0 | 30 | 60 | 90 | 120 | 150 | ||
| 180 | 210 | 240 | 270 | 300 | 330 | 360 | |
 |
Let us look back at our values for
| 1 | 0 |
If you look carefully, you will notice that the cosine of an angle is the same as the sine of the angle . Take for example,
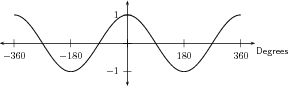
This tells us that in order to create the cosine graph, all we need to do is to shift the sine graph to the left. The graph of is shown in [link] . As the cosine graph is simply a shifted sine graph, it will have the same period and amplitude as the sine graph.
In the equation, , and are constants and have different effects on the graph of the function. The general shape of the graph of functions of this form is shown in [link] for the function .
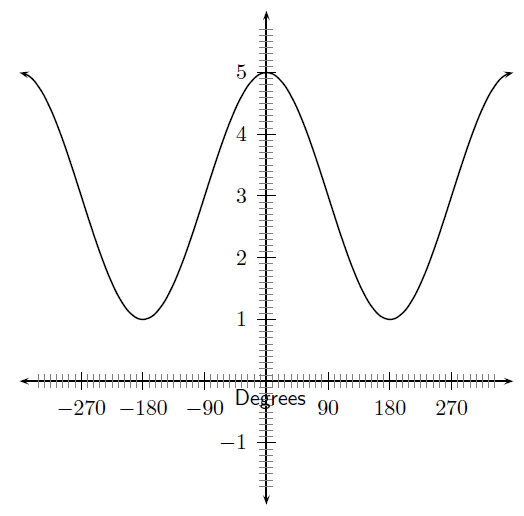
You should have found that the value of affects the amplitude of the cosine graph in the same way it did for the sine graph.
You should have also found that the value of shifts the cosine graph in the same way as it did the sine graph.
These different properties are summarised in [link] .
|
|
| |
|
|
|
For , the domain is because there is no value of for which is undefined.
It is easy to see that the range of will be the same as the range of . This is because the maximum and minimum values of will be the same as the maximum and minimum values of .
The -intercept of is calculated in the same way as for sine.
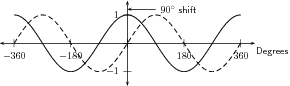
Notice that the two graphs look very similar. Both oscillate up and down around the -axis as you move along the axis. The distances between the peaks of the two graphs is the same and is constant along each graph. The height of the peaks and the depths of the troughs are the same.
The only difference is that the graph is shifted a little to the right of the graph by 90 . That means that if you shift the whole graph to the right by 90 it will overlap perfectly with the graph. You could also move the graph by 90 to the left and it would overlap perfectly with the graph. This means that:
Complete the following table, using your calculator to calculate the values correct to 1 decimal place. Then plot the values with on the -axis and on the -axis.
| 0 | 30 | 60 | 90 | 120 | 150 | ||
| 180 | 210 | 240 | 270 | 300 | 330 | 360 | |
 |

Notification Switch
Would you like to follow the 'Basic mathematics review' conversation and receive update notifications?