10.6 Gauge pressure, absolute pressure, and pressure measurement (Page 3/7)

<< Chapter < Page

College physics ii Page 3 / 7

Chapter >> Page >

Systolic pressure

Systolic pressure is the maximum blood pressure.

Diastolic pressure

Diastolic pressure is the minimum blood pressure.

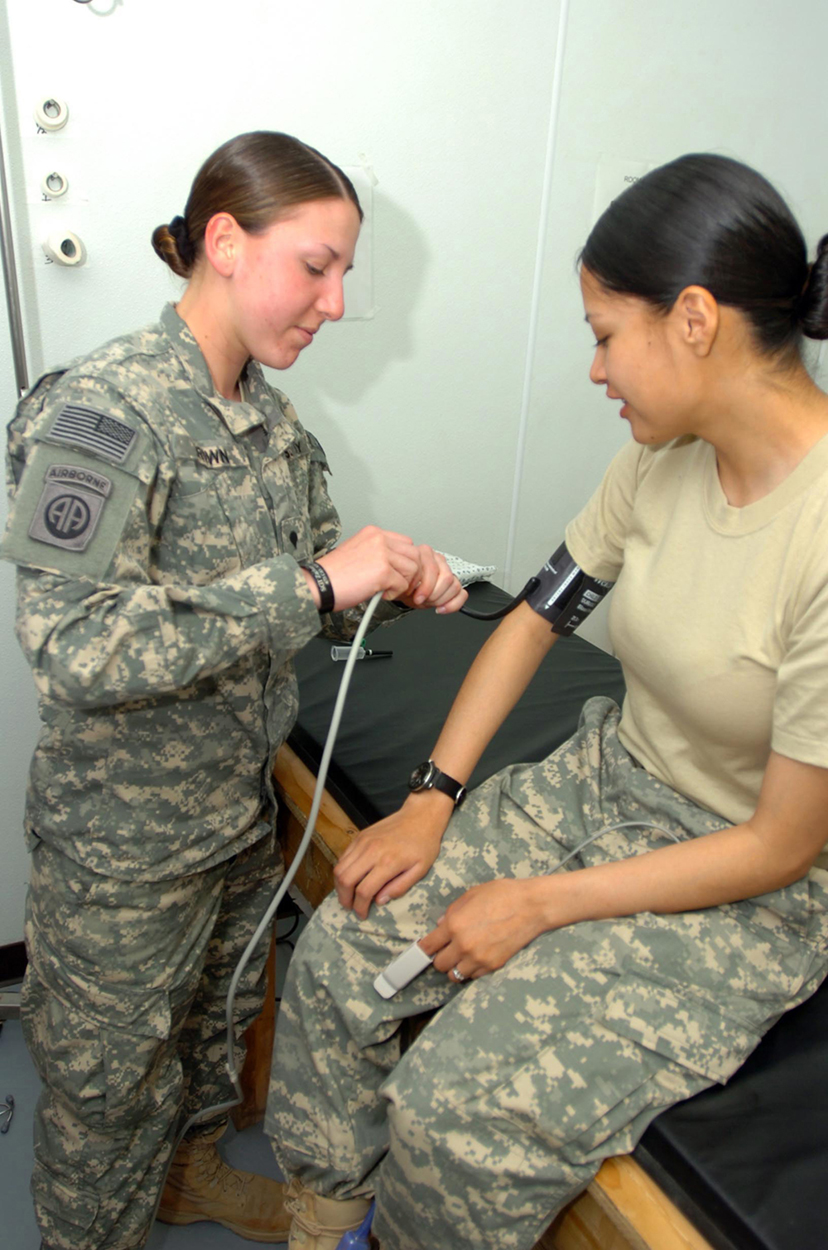
U.S. Army Spc. Monica Brown takes a soldier's blood pressure reading at the hospital on Forward Operating Base Salerno, Afghanistan, March 10, 2008. — In routine blood pressure measurements, an inflatable cuff is placed on the upper arm at the same level as the heart. Blood flow is detected just below the cuff, and corresponding pressures are transmitted to a mercury-filled manometer. (credit: U.S. Army photo by Spc. Micah E. Clare\4TH BCT)

Calculating height of iv bag: blood pressure and intravenous infusions

Intravenous infusions are usually made with the help of the gravitational force. Assuming that the density of the fluid being administered is 1.00 g/ml, at what height should the IV bag be placed above the entry point so that the fluid just enters the vein if the blood pressure in the vein is 18 mm Hg above atmospheric pressure? Assume that the IV bag is collapsible.

Strategy for (a)

For the fluid to just enter the vein, its pressure at entry must exceed the blood pressure in the vein (18 mm Hg above atmospheric pressure). We therefore need to find the height of fluid that corresponds to this gauge pressure.

Solution

We first need to convert the pressure into SI units. Since $1.0 mm Hg = 133 Pa$ ,

P = 18 mm Hg \times \frac{133 Pa}{1.0 mm Hg} = 2400 Pa .

Rearranging $P_{g} = hρg$ for $h$ gives $h = \frac{P_{g}}{ρg}$ . Substituting known values into this equation gives

\begin{array}{l} h & = & \frac{2400 N {/m}^{2}}{(1 . 0 \times 10^{3} {kg/m}^{3}) (9.80 {m/s}^{2})} \\ = & 0.24 m. \end{array}

Discussion

The IV bag must be placed at 0.24 m above the entry point into the arm for the fluid to just enter the arm. Generally, IV bags are placed higher than this. You may have noticed that the bags used for blood collection are placed below the donor to allow blood to flow easily from the arm to the bag, which is the opposite direction of flow than required in the example presented here.

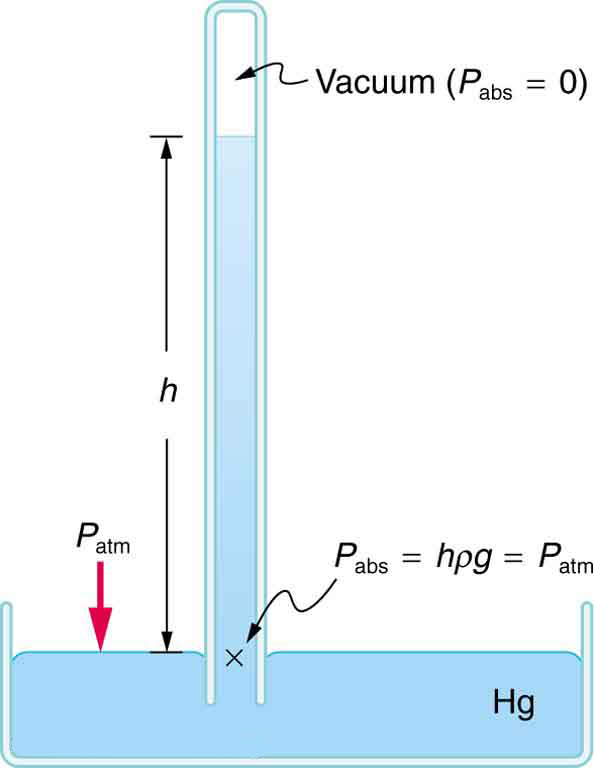
A barometer is a device that measures atmospheric pressure. A mercury barometer is shown in [link] . This device measures atmospheric pressure, rather than gauge pressure, because there is a nearly pure vacuum above the mercury in the tube. The height of the mercury is such that $hρg = P_{atm}$ . When atmospheric pressure varies, the mercury rises or falls, giving important clues to weather forecasters. The barometer can also be used as an altimeter, since average atmospheric pressure varies with altitude. Mercury barometers and manometers are so common that units of mm Hg are often quoted for atmospheric pressure and blood pressures. [link] gives conversion factors for some of the more commonly used units of pressure.

Mercury barometer has an evacuated glass tube inverted and placed in the mercury container. The height of the mercury column in the inverted tube is determined by the atmospheric pressure. — A mercury barometer measures atmospheric pressure. The pressure due to the mercury’s weight, $hρg$ , equals atmospheric pressure. The atmosphere is able to force mercury in the tube to a height $h$ because the pressure above the mercury is zero.

Conversion factors for various pressure units
Conversion to N/m ² (Pa)	Conversion from atm
$1.0 atm = 1 . 013 \times 10^{5} {N/m}^{2}$	$1.0 atm = 1 . 013 \times 10^{5} {N/m}^{2}$
$1.0 {dyne/cm}^{2} = 0 . 10 {N/m}^{2}$	$1.0 atm = 1 . 013 \times 10^{6} {dyne/cm}^{2}$
$1.0 {kg/cm}^{2} = 9 . 8 \times 10^{4} {N/m}^{2}$	$1.0 atm = 1 . 013 {kg/cm}^{2}$
$1.0 lb/in .^{2} = 6 . 90 \times 10^{3} {N/m}^{2}$	$1.0 atm = 14 . 7 lb/in .^{2}$
$1.0 mm Hg = 133 {N/m}^{2}$	$1.0 atm = 760 mm Hg$
$1 . 0 cm Hg = 1 . 33 \times 10^{3} {N/m}^{2}$	$1.0 atm = 76 . 0 cm Hg$
$1 . 0 cm water = 98 . 1 {N/m}^{2}$	$1.0 atm = 1 . 03 \times 10^{3} cm water$
$1.0 bar = 1 . 000 \times 10^{5} {N/m}^{2}$	$1.0 atm = 1.013 bar$
$1.0 millibar = 1 . 000 \times 10^{2} {N/m}^{2}$	$1.0 atm = 1013 millibar$

Section summary

Gauge pressure is the pressure relative to atmospheric pressure.
Absolute pressure is the sum of gauge pressure and atmospheric pressure.
Aneroid gauge measures pressure using a bellows-and-spring arrangement connected to the pointer of a calibrated scale.
Open-tube manometers have U-shaped tubes and one end is always open. It is used to measure pressure.
A mercury barometer is a device that measures atmospheric pressure.

Conceptual questions

Explain why the fluid reaches equal levels on either side of a manometer if both sides are open to the atmosphere, even if the tubes are of different diameters.

[link] shows how a common measurement of arterial blood pressure is made. Is there any effect on the measured pressure if the manometer is lowered? What is the effect of raising the arm above the shoulder? What is the effect of placing the cuff on the upper leg with the person standing? Explain your answers in terms of pressure created by the weight of a fluid.

Considering the magnitude of typical arterial blood pressures, why are mercury rather than water manometers used for these measurements?

Problems&Exercises

Find the gauge and absolute pressures in the balloon and peanut jar shown in [link] , assuming the manometer connected to the balloon uses water whereas the manometer connected to the jar contains mercury. Express in units of centimeters of water for the balloon and millimeters of mercury for the jar, taking $h = 0 . 0500 m$ for each.

Balloon:

$\begin{array}{l} P_{g} & = & 5.00 cm H_{2} O, \\ P_{abs} & = & 1.035 \times 10^{3} cm H_{2} O. \end{array}$

Jar:

$\begin{array}{l} P_{g} & = & - 50.0 mm Hg, \\ P_{abs} & = & 710 mm Hg. \end{array}$

(a) Convert normal blood pressure readings of 120 over 80 mm Hg to newtons per meter squared using the relationship for pressure due to the weight of a fluid $(P = hρg)$ rather than a conversion factor. (b) Discuss why blood pressures for an infant could be smaller than those for an adult. Specifically, consider the smaller height to which blood must be pumped.

How tall must a water-filled manometer be to measure blood pressures as high as 300 mm Hg?

4.08 m

Pressure cookers have been around for more than 300 years, although their use has strongly declined in recent years (early models had a nasty habit of exploding). How much force must the latches holding the lid onto a pressure cooker be able to withstand if the circular lid is $25.0 cm$ in diameter and the gauge pressure inside is 300 atm? Neglect the weight of the lid.

Suppose you measure a standing person’s blood pressure by placing the cuff on his leg 0.500 m below the heart. Calculate the pressure you would observe (in units of mm Hg) if the pressure at the heart were 120 over 80 mm Hg. Assume that there is no loss of pressure due to resistance in the circulatory system (a reasonable assumption, since major arteries are large).

$\begin{matrix} Δ P = 38.7 mm Hg, \\ Leg blood pressure = \frac{159}{119} . \end{matrix}$

A submarine is stranded on the bottom of the ocean with its hatch 25.0 m below the surface. Calculate the force needed to open the hatch from the inside, given it is circular and 0.450 m in diameter. Air pressure inside the submarine is 1.00 atm.

Assuming bicycle tires are perfectly flexible and support the weight of bicycle and rider by pressure alone, calculate the total area of the tires in contact with the ground. The bicycle plus rider has a mass of 80.0 kg, and the gauge pressure in the tires is $3 . 50 \times 10^{5} Pa$ .

$22.4 {cm}^{2}$

<< Chapter < Page Page > Chapter >>

Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, College physics ii. OpenStax CNX. Nov 29, 2012 Download for free at http://legacy.cnx.org/content/col11458/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics ii' conversation and receive update notifications?

Ask

	28 AP 28 Development Inheritance MCQ By OpenStax Start Quiz
	Clinical Issues in TB Management By Cath Yu Start Quiz
	Young Economist MCQ Test By Robert Murphy Start Test
	Anthropology Religion Culture By Richley Crapo Start Assignment
	Anthropology Marriage Family Household By Richley Crapo Start Assignment
	10 Biology 10 Cell Reproduction MCQ By OpenStax Start Quiz
	24 PLANT QUIZ 1 By Brooke Delaney Start Exam
	Human A&P 2- Final By Madison Christian Start Flashcards
	Professional Writing MCQ By Mary Cohen Start Quiz
	2 Neuroanatomy 02 Brain External Features By Stephen Voron Start Quiz