| << Chapter < Page | Chapter >> Page > |
Điểm cực đại địa phương (a local maximum) : là một trạng thái tốt hơn tất cả lân cận của nó nhưng không tốt hơn một số trạng thái khác ở xa hơn. Nghĩa là tại một điểm cực đại địa phương, mọi trạng thái trong một lân cận của trạng thái hiện tại đều xấu hơn trạng thái hiện tại. Tuy có dáng vẻ của lời giải nhưng các cực đại địa phương không phải là lời giải thực sự. Trong trường hợp này, chúng được gọi là những ngọn đồi thấp.
Đoạn đơn điệu ngang (a plateau) : là một vùng bằng phẳng của không gian tìm kiếm, trong đó, toàn bộ các trạng thái lân cận đều có cùng giá trị.
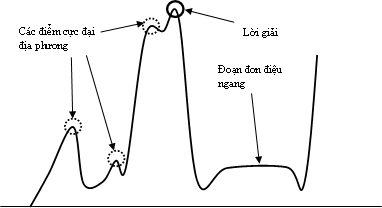
Hình : Các tình huống khó khăn cho tìm kiếm leo đèo.
Để đối phó với các các điểm này, người ta đã đưa ra một số giải pháp. Ta sẽ tìm hiểu 2 trong số các giải pháp này. Những giải này, không thực sự giải quyết trọn vẹn vấn đề mà chỉ là một phương án cứu nguy tạm thời mà thôi.
Phương án đầu tiên là kết hợp leo đồi và quay lui. Ta sẽ quay lui lại các trạng thái trước đó và thử đi theo hướng khác. Thao tác này hợp lý nếu tại các trạng thái trước đó có một hướng đi tốt mà ta đã bỏ qua trước đó. Đây là một cách khá hay để đối phó với các điểm cực đại địa phương. Tuy nhiên, do đặc điểm của leo đồi là "bước sau cao hơn bước trước" nên phương án này sẽ thất bại khi ta xuất phát từ một điểm quá cao hoặc xuất phát từ một đỉnh đồi mà để đến được lời giải cần phải đi qua một "thung lũng" thật sâu như trong hình sau.
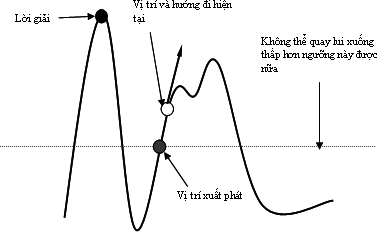
Hình : Một trường hợp thất bại của leo đèo kết hợp quay lui.
Cách thứ hai là thực hiện một bước nhảy vọt theo hướng nào đó để thử đến một vùng mới của không gian tìm kiếm. Nôm na là "bước" liên tục nhiều "bước" (chẳng hạn 5,7,10, …) mà tạm thời "quên" đi việc kiểm tra "bước sau cao hơn bước trước". Tiếp cận có vẻ hiệu quả khi ta gặp phải một đoạn đơn điệu ngang. Tuy nhiên, nhảy vọt cũng có nghĩa là ta đã bỏ qua cơ hội để tiến đến lời giải thực sự. Trong trường hợp chúng ta đang đứng khá gần lời giải, việc nhảy vọt sẽ đưa chúng ta sang một vị trí hoàn toàn xa lạ, mà từ đó, có thể sẽ dẫn chúng ta đến một rắc rối kiểu khác. Hơn nữa, số bước nhảy là bao nhiêu và nhảy theo hướng nào là một vấn đề phụ thuộc rất nhiều vào đặc điểm không gian tìm kiếm của bài toán.
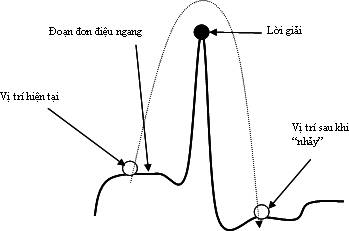
Hình Một trường hợp khó khăn cho phương án "nhảy vọt".
Leo núi là một phương pháp cục bộ bởi vì nó quyết định sẽ làm gì tiếp theo dựa vào một đánh giá về trạng thái hiện tại và các trạng thái kế tiếp có thể có (tốt hơn trạng thái hiện tại, trạng thái tốt nhất tốt hơn trạng thái hiện tại) thay vì phải xem xét một cách toàn diện trên tất cả các trạng thái đã đi qua. Thuận lợi của leo núi là ít gặp sự bùng nổ tổ hợp hơn so với các phương pháp toàn cục. Nhưng nó cũng giống như các phương pháp cục bộ khác ở chỗ là không chắc chắn tìm ra lời giải trong trường hợp xấu nhất.
Một lần nữa, ta khẳng định lại vai trò quyết định của hàm Heuristic trong quá trình tìm kiếm lời giải. Với cùng một thuật giải (như leo đồi chẳng hạn), nếu ta có một hàm Heuristic tốt hơn thì kết quả sẽ được tìm thấy nhanh hơn. Ta hãy xét bài toán về các khối được trình bày ở hình sau. Ta có hai thao tác biến đổi là:

Notification Switch
Would you like to follow the 'Lập trình và ngôn ngữ lập trình' conversation and receive update notifications?