| << Chapter < Page | Chapter >> Page > |
Đồ hình truyền tín hiệu ( signal flow graph - ĐHTTH) được giới thiệu đầu tiên bởi S.J. MASON được xem như là ký hiệu đơn giản hóa của sơ đồ khối, để trình bày mối tương quan nhân quả của một hệ tuyến tính.
Bên cạnh sự khác biệt về hình trạng vật lý giữa ĐHTTH và sơ đồ khối, ta có thể thấy ĐHTTH chặc chẽ hơn về những liên hệ toán học. Nhưng những định luật dùng cho sơ đồ khối thì mềm dẻo hơn nhiều và kém rõ ràng hơn.
Một ĐHTTH được định nghĩa như là một phương pháp đồ họa để miêu tả những liên hệ vào - ra giữa các biến của một tập hợp những phương trình đại số.
Xem một hệ tuyến tính được diễn tả bởi tập hợp N phương trình đại số.
j= 1,2.3...N (3.1)
N phương trình nầy được viết dưới dạng tương quan nhân quả:
Háûu quaí thỉï j = (âäü låüi tỉì k âãún j) . (nguyãn nhán thỉï k) (3.2)k=1N
Hay đơn giản hơn:
Output = (độ lợi).(input) (3.3)
Đồ hình truyền tín hiệu được vẽ dựa vào tiên đề quan trọng nhất này.
Trường hợp hệ thống được mô tả bằng các phương trình vi tích phân, trước nhất ta phải biến đổi chúng thành các phương trình biến đổi Laplace và sắp xếp chúng theo dạng phương trình (3.1).
j=1,2,.... ,N (3.4)
Khi vẽ ĐHTTH , các điểm nối hay là nút dùng để biểu diển các biến yj hay yk . Các nút được nối với nhau bởi các đoạn thẳng gọi là nhánh, tuỳ thuộc vào các phương trình nhân quả. Các nhánh được đặc trưng bởi độ lợi nhánh và chiều. Một tín hiệu chỉ có thể truyền ngang qua nhánh theo chiều mũi tên.
Thí dụ, xem một hệ tuyến tính được trình bài bởi phương trình đơn giản.
y2 =a12 .y1 (3.5)
Trong đó, y1 là biến s vào , y2 là biến ra và a12 là độ lợi hay độ truyền dẫn (transmittansce) giữa hai biến số.
Đồ hình truyền tín hiệu biểu diển cho phương trình (3.5) được vẽ ở hình H.3_1.
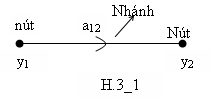
Chiều của nhánh từ nút y1 đến nút y2 chỉ sự phụ thuộc của biến ra với biến vào, và không có ngược lại. Vì thế, mặc dù phương trình (3.5) có thể viết lại:
Nhưng ĐHTTH ở hình H.3_1 không đưa đến một tương quan như vậy. Nếu phương trình (3.6) có giá trị như là một tương quan nhân quả theo ý nghĩa vật lý, thì phải vẽ một ĐHTTH khác.
Một thí dụ khác, xem tập hợp các phương trình đại số :
y2 = a12 y1 + a32 y3
y3 = a23 y2 + a43 y4
y4 = a24 y2 + a34 y3 + a44 y4 (3.7)
y5 = a25 y2 + a45 y4
ĐHTTH cho các phương trình này được vẽ từng bước như hình H.3_2. Các nút biểu diễn các biến y1 , y2 , y3 , y4 và y5 được đặt theo thứ tự từ trái sang phải.
a)
b)
c)
d)
H.3_2. : ĐHTTH của hệ phương trình (3.7) .
1) Nút vào (nguồn ) : Nút vào là một nút chỉ có những nhánh ra. Thí dụ nút y1 ở H.3_2 .
2) Nút ra : Nút ra là nút chỉ có những nhánh vào. Thí dụ nút y5 ở H.3_2.
Tuy nhiên không phải lúc nào cũng có sẵn nút ra thỏa định nghĩa trên. Thí dụ ĐHTTH ở hình H.3_3a. Ởû đó không có nút nào phù hợp định nghĩa. Tuy nhiên, có thể xem y3 và/hoặc y2 là nút ra nếu ta đưa vào các nhánh với độ lợi đơn vị cho các biến y3 và y2 như H.3_3b. Các nút đưa thêm vào gọi là nút giả (dummy node).

Notification Switch
Would you like to follow the 'Cơ sở tự động học' conversation and receive update notifications?