3.3 Chebyshev filter properties

The design of a chebyshev lowpass filter.

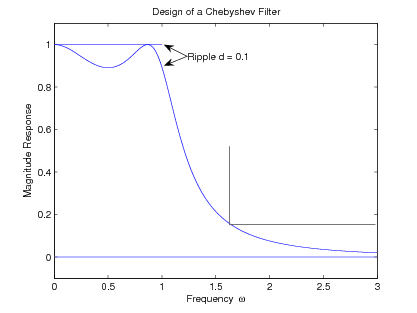
The design specifications require a maximum passband ripple of $\delta =0.1$ or $a=0.91515$ dB, and can allow no greater response than $G=0.2$ for frequencies above ${\omega }_s=1.6$ radians per second.

Given $\delta =0.1$ or $a=0.91515$ , equation [link] implies

$$ϵ=0.484322$$

Given $G=0.2$ and ${\omega }_s=1.6$ , equation [link] implies an order of $N=3$ . From $ϵ$ and $N$ , ${\nu }_0$ is 0.49074 from [link] and

$$sinh\left({\nu }_0\right)=0.510675$$

$$cosh\left({\nu }_0\right)=1.122849$$

These multipliers are used to scale the root locations of the example third-order Butterworth filter to give

$$F\left(s\right)=\frac{1}{(s+0.51067)(s+0.25534+j0.97242)(s+0.25534-j0.97242)}$$

$$F\left(s\right)=\frac{1}{(s+0.51067)(s^2+0.510675s+1.010789)}$$

$$F\left(s\right)=\frac{1}{s^3+102135s^2+1.271579s+0.516185}$$

The frequency response is shown in [link]

Inverse-chebyshev filter properties

A second form of the mixture of a Chebyshev approximation and a Taylor's series approximation is called the Inverse Chebyshev filteror the Chebyshev II filter. This error measure uses a Taylor's series for the passband just as for the Butterworth filter and minimizes the maximumerror over the total stopband. It reverses the types of approximation usedin the preceding section. A fifth-order example is illustrated in Figure 1c from Design of Infinite Impulse Response (IIR) Filters by Frequency Transformations and [link] c.

Rather than developing the approximation directly, it is easier to modify the results from the regular Chebyshev filter. First, thefrequency variable $\omega$ in the regular Chebyshev filter, described in [link] , is replaced by $1/\omega$ , which interchanges the characteristics at $\omega$ equals zero and infinity and does not change the performance at $\omega$ equals unity. This converts a Chebyshev lowpass filter into a Chebyshev highpass filter as illustrated in [link] moving from the first to second frequency response.

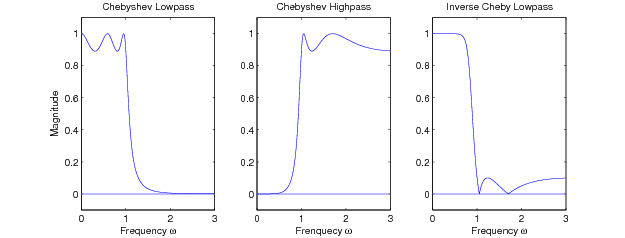
This highpass characteristic is subtracted from unity to give the desired lowpass inverse-Chebyshev frequency response illustrated in [link] c. The resulting magnitude-squared frequency- response function is given by

Zero locations

The zeros of the Chebyshev polynomial $C_N\left(\omega \right)$ are easily found by

which requires

for $k=0,1,\cdots N-1$ , or

for $k=0,\pm 2,\pm 4,...,\pm (N-1)$ : N odd

$k=\pm 1,\pm 3,\pm 5,...,\pm (N-1)$ : N even

The zeros of the inverse-Chebyshev filter transfer function are derived from [link] and [link] to give

The zero locations are not a function of $ϵ$ , i.e., they are independent of the stopband ripple.

Pole locations

The pole locations are the reciprocal of those for the regular Chebyshev filter. If the polesfor the inverse filter are denoted by

the locations are

Although this gives a straightforward formula for calculating the location of the poles and zeros of the inverse-Chebyshev filter, they do not lie on a simple geometric curve as did those for the Butterworth and Chebyshev filters. Note thatthe conditions for a Taylor's series approximation with preset zero locations are satisfied.