3.3 Chebyshev filter properties

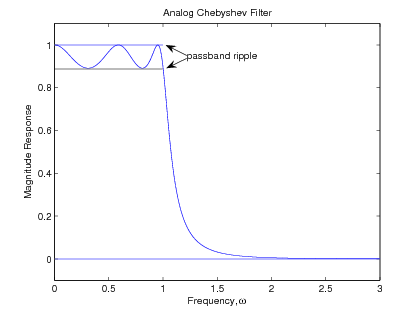
The approximation parameters must be clearly understood. The passband ripple is defined to be the difference between the maximumand the minumum of $\left|F\right|$ over the passband frequencies of $0<\omega <1$ . There can be confusion over this point as two definitions appear in the literature. Most digital [link] , [link] , [link] , [link] and analog [link] filter design books use the definition just stated. Approximation literature, especiallyconcerning FIR filters, use one half this value which is a measure of the maximum error, $\left|\right|F|-|F_d\left|\right|$ , where $|F_d|$ is the center line in the passband of [link] , which $\left|F\right|$ oscillates around.

The Chebyshev theory states that the maximum error over that band is minimum and that this optimal approximation function hasequal ripple over the pass band. It is easy to see that e in [link] determines the ripple in the passband and the order $N$ determines the rate that the response goes to zero as $\omega$ goes to infinity.

Pole locations

A method for finding the pole locations for the Chebyshev filter transfer function is next developed. The details of thissection can be skipped and the results in [link] , [link] used if desired.

From [link] , it is seen that the poles of $FF\left(s\right)$ occur when

or

From [link] , define $\phi ={cos}^{-1}\left(\omega \right)$ with real and imaginary parts given by

This gives,

which implies the real part of $C_N$ is zero. This requires

which implies

which in turn implies that $u$ takes on values of

For these values of $u$ , $sin\left(nu\right)=\pm 1$ , we have

which requires $\nu$ to take on a value of

Using $s=j\omega$ gives

which gives the location of the $N$ poles in the $s$ plane as

where

for $N$ values of $k$ where

A partially factored form for F(s) can be derived using the same approach as for the Butterworth filter. For N even, the form is

for $k=1,3,5,\cdots ,N-1$ . For $N$ odd, $F\left(s\right)$ has a single real pole and, therefore, the form

for $k=2,4,6,...,N-1$ This is a convenient form for the cascade and parallel realizations.

A single formula for both even and odd N is

for $N$ values of $k$ where $k=0,1,2,\cdots ,N-1$

Note the similarity to the pole locations for the Butterworth filter. Cross multiplying, squaring, and adding the terms in [link] , [link] gives

This is the equation for an ellipse and shows that the poles of a Chebyshev filter lie on an ellipse similarto the way the poles of a Butterworth filter lie on a circle [link] , [link] , [link] , [link] , [link] , [link] .

Summary

This section has developed the classical Chebyshev filter approximation which minimizes the maximum error over the passbandand uses a Taylor's series approximation at infinity. This results in the error being equal ripple in the passband. Thetransfer function was developed in terms of the Chebyshev polynomial and explicit formulas were derived for the location ofthe transfer function poles. These can be expressed as a modification of the pole locations for the Butterworth filter andare implemented in the appendix.