10.2 The trig functions for any angle and applications  (Page 2/2)

Solving simple trigonometric equations

Using what we have learnt about trig functions we can now solve some simple trig equations. We use the principles from Equations and Inequalities to help us solve trig equations.

Simple applications of trigonometric functions

Trigonometry was probably invented in ancient civilisations to solve practical problems such as building construction and navigating by the stars. In this section we will show how trigonometry can be used to solve some other practical problems.

Height and depth

One simple task is to find the height of a building by using trigonometry. We could just use a tape measure lowered from the roof, but this is impractical (and dangerous) for tall buildings. It is much more sensible to measure a distance along the ground and use trigonometry to find the height of the building.

[link] shows a building whose height we do not know. We have walked 100 m away from the building and measured the angle from the ground up to the top of the building. This angle is found to be $38,7^{\circ }$ . We call this angle the angle of elevation . As you can see from [link] , we now have a right-angled triangle. As we know the length of one side and an angle, we can calculate the height of the triangle, which is the height of the building we are trying to find.

If we examine the figure, we see that we have the opposite and the adjacent of the angle of elevation and we can write:

A block of flats is 100m away from a cellphone tower. Someone stands at $B$ . They measure the angle from $B$ up to the top of the tower $E$ to be 62 ${}^{\circ }$ . This is the angle of elevation. They then measure the angle from $B$ down to the bottom of the tower at $C$ to be 34 ${}^{\circ }$ . This is the angle of depression.What is the height of the cellph one tower correct to 1 decimal place?

1. Identify a strategy

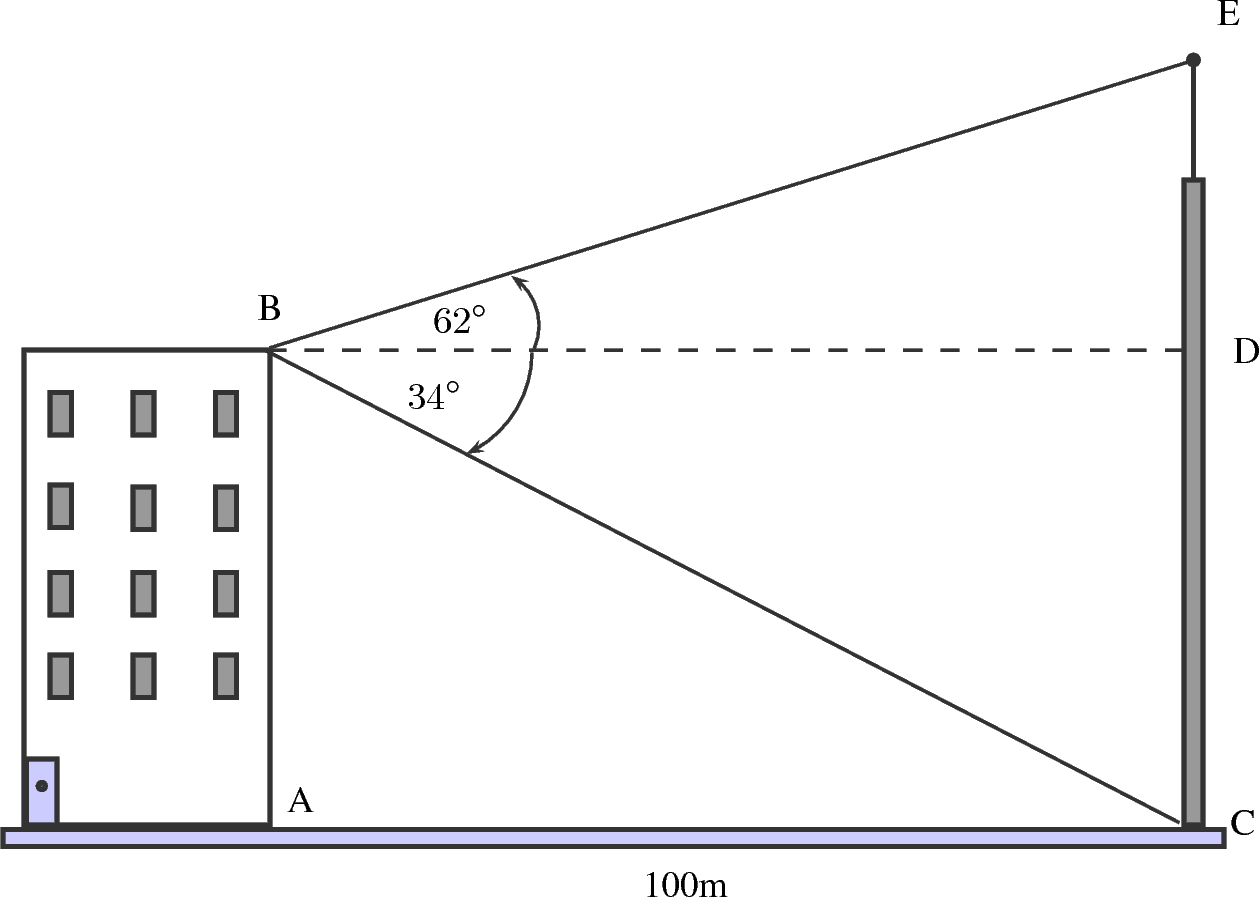
   To find the height of the tower, all we have to do is find the length of $CD$ and $DE$ . We see that $▵BDE$ and $▵BDC$ are both right-angled triangles. For each of the triangles, we have an angle and we have the length $AD$ . Thus we can calculate the sides of the triangles.

2. Calculate $CD$

   We are given that the length $AC$ is 100m. $CABD$ is a rectangle so $BD=AC=100\mathrm{m}$ .

   $$\begin{array}{ccc}\hfill tan\left(C\widehat{B}D\right)& =& \frac{CD}{BD}\hfill \\ \hfill \Rightarrow CD& =& BD\times tan\left(C\widehat{B}D\right)\hfill \\ & =& 100\times tan{34}^{\circ }\hfill \end{array}$$

   Use your calculator to find that $tan{34}^{\circ }=0,6745$ . Using this, we find that $CD=67,45$ m

3. Calculate $DE$
   $$\begin{array}{ccc}\hfill tan\left(D\widehat{B}E\right)& =& \frac{DE}{BD}\hfill \\ \hfill \Rightarrow DE& =& BD\times tan\left(D\widehat{B}E\right)\hfill \\ & =& 100\times tan{62}^{\circ }\hfill \\ & =& 188,07\mathrm{m}\hfill \end{array}$$
4. Combine the previous answers

   We have that the height of the tower $CE=CD+DE=67,45\mathrm{m}+188,07\mathrm{m}=255.5\mathrm{m}$ .

Got questions? Get instant answers now!

Maps and plans

Maps and plans are usually scale drawings. This means that they are an exact copy of the real thing, but are usually smaller. So, only lengths are changed, but all angles are the same. We can use this idea to make use of maps and plans by adding information from the real world.

A ship approaching Cape Town Harbour reaches point A on the map, due south of Pretoria and due east of Cape Town. If the distance from Cape Town to Pretoria is 1000km, use trigonometry to find out how far east the ship is from Cape Town, and hence find the scale of the map.

1. Identify what happens in the question

   We already know the distance between Cape Town and $A$ in blocks from the given map (it is 5 blocks). Thus if we work out how many kilometers this same distance is, we can calculate how many kilometers each block represents, and thus we have the scale of the map.

2. Identify given information

   Let us denote Cape Town with $C$ and Pretoria with $P$ . We can see that triangle $APC$ is a right-angled triangle. Furthermore, we see that the distance $AC$ and distance $AP$ are both 5 blocks. Thus it is an isoceles triangle, and so $A\widehat{C}P=A\widehat{P}C={45}^{\circ }$ .

3. Carry out the calculation
   $$\begin{array}{cc}\hfill CA=& CP\times cos\left(A\widehat{C}P\right)\\ \hfill =& 1000\times cos\left({45}^{\circ }\right)\\ \hfill =& \frac{1000}{\sqrt{2}}\mathrm{km}\end{array}$$

   To work out the scale, we see that

   $$\begin{array}{cc}\hfill 5\text{blocks}=& \frac{1000}{\sqrt{2}}\text{km}\\ \hfill \Rightarrow 1\text{block}=& \frac{200}{\sqrt{2}}\text{km}\end{array}$$

Got questions? Get instant answers now!

Mr Nkosi has a garage at his house, and he decides that he wants to add a corrugated iron roof to the side of the garage. The garage is 4m high, and his sheet for the roof is 5m long. If he wants the roof to be at an angle of $5^{\circ }$ , how high must he build the wall $BD$ , which is holding up the roof? Give the answer to 2 decimal places.

1. Set out strategy

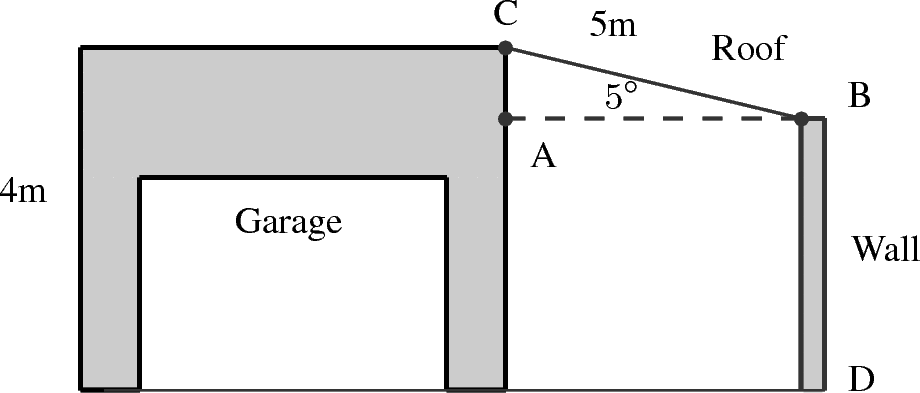
   We see that the triangle $ABC$ is a right-angled triangle. As we have one side and an angle of this triangle, we can calculate $AC$ . The height of the wall is then the height of the garage minus $AC$ .

2. Execute strategy

   If $BC$ =5m, and angle $A\widehat{B}C=5^{\circ }$ , then

   $$\begin{array}{ccc}\hfill AC& =& BC\times sin\left(A\widehat{B}C\right)\hfill \\ & =& 5\times sin{5}^{\circ }\hfill \\ & =& 5\times 0,0871\hfill \\ & =& 0.4358\mathrm{m}\hfill \end{array}$$

   Thus we have that the height of the wall $BD=4\mathrm{m}-0.4358\mathrm{m}=3.56\mathrm{m}$ .

Got questions? Get instant answers now!

Applications of trigonometric functions

1. A boy flying a kite is standing 30 m from a point directly under the kite. If the string to the kite is 50 m long, find the angle ofelevation of the kite.
   
2. What is the angle of elevation of the sun when a tree 7,15 m tall casts a shadow 10,1 m long?