| << Chapter < Page | Chapter >> Page > |
Solve the equation exactly using an identity:
If we rewrite the right side, we can write the equation in terms of cosine:
Our solutions are
Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as or When confronted with these equations, recall that is a horizontal compression by a factor of 2 of the function On an interval of we can graph two periods of as opposed to one cycle of This compression of the graph leads us to believe there may be twice as many x -intercepts or solutions to compared to This information will help us solve the equation.
Solve exactly: on
We can see that this equation is the standard equation with a multiple of an angle. If we know is in quadrants I and IV. While will only yield solutions in quadrants I and II, we recognize that the solutions to the equation will be in quadrants I and IV.
Therefore, the possible angles are and So, or which means that or Does this make sense? Yes, because
Are there any other possible answers? Let us return to our first step.
In quadrant I, so as noted. Let us revolve around the circle again:
so
One more rotation yields
so this value for is larger than so it is not a solution on
In quadrant IV, so as noted. Let us revolve around the circle again:
so
One more rotation yields
so this value for is larger than so it is not a solution on
Our solutions are Note that whenever we solve a problem in the form of we must go around the unit circle times.
We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem . We begin with the familiar Pythagorean Theorem, and model an equation to fit a situation.
Use the Pythagorean Theorem, and the properties of right triangles to model an equation that fits the problem.
One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is 69.5 meters above the ground, and the second anchor on the ground is 23 meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)? See [link] .
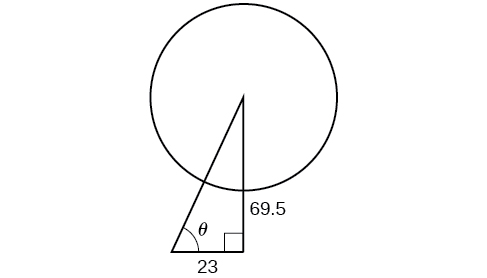
Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.
The angle of elevation is formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.
The angle of elevation is approximately and the length of the cable is 73.2 meters.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?