| << Chapter < Page | Chapter >> Page > |
OSHA safety regulations require that the base of a ladder be placed 1 foot from the wall for every 4 feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.
For any length of ladder, the base needs to be a distance from the wall equal to one fourth of the ladder’s length. Equivalently, if the base of the ladder is “ a” feet from the wall, the length of the ladder will be 4 a feet. See [link] .
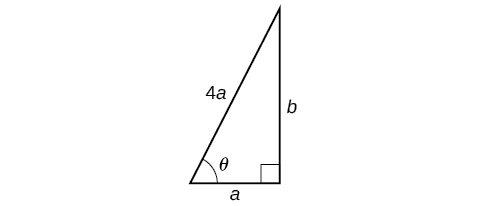
The side adjacent to is a and the hypotenuse is Thus,
The elevation of the ladder forms an angle of with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:
Thus, the ladder touches the wall at feet from the ground.
Access these online resources for additional instruction and practice with solving trigonometric equations.
Will there always be solutions to trigonometric function equations? If not, describe an equation that would not have a solution. Explain why or why not.
There will not always be solutions to trigonometric function equations. For a basic example,
When solving a trigonometric equation involving more than one trig function, do we always want to try to rewrite the equation so it is expressed in terms of one trigonometric function? Why or why not?
When solving linear trig equations in terms of only sine or cosine, how do we know whether there will be solutions?
If the sine or cosine function has a coefficient of one, isolate the term on one side of the equals sign. If the number it is set equal to has an absolute value less than or equal to one, the equation has solutions, otherwise it does not. If the sine or cosine does not have a coefficient equal to one, still isolate the term but then divide both sides of the equation by the leading coefficient. Then, if the number it is set equal to has an absolute value greater than one, the equation has no solution.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?