This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses fractions of whole numbers. By the end of the module students should be able to understand the concept of fractions of whole numbers and recognize the parts of a fraction.
Section overview
- More Numbers on the Number Line
- Fractions of Whole Numbers
- The Parts of a Fraction
- Reading and Writing Fractions
More numbers on the number line
In Chapters
[link] ,
[link] , and
[link] , we studied the whole numbers and methods of combining them. We noted that we could visually display the whole numbers by drawing a number line and placing closed circles at whole number locations.

By observing this number line, we can see that the whole numbers do not account for every point on the line. What numbers, if any, can be associated with these points? In this section we will see that many of the points on the number line, including the points already associated with whole numbers, can be associated with numbers called
fractions .
Fractions of whole numbers
The nature of the positive fractions
We can extend our collection of numbers, which now contains only the whole numbers, by including fractions of whole numbers. We can determine the nature of these fractions using the number line.
If we place a pencil at some whole number and proceed to travel to the right to the next whole number, we see that our journey can be
broken into different types of equal parts as shown in the following examples.
-
1 part.
-
2 equal parts.

-
3 equal parts.

-
4 equal parts.

The latin word fractio
Notice that the number of parts, 2, 3, and 4, that we are breaking the original quantity into is always a
nonzero whole number . The idea of breaking up a whole quantity gives us the word
fraction . The word fraction comes from the Latin word "fractio" which means a breaking, or fracture.
Suppose we break up the interval from some whole number to the next whole number into five equal parts.
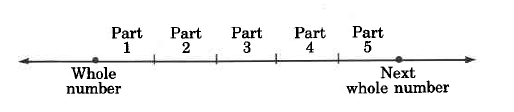
After starting to move from one whole number to the next, we decide to stop after covering only two parts. We have covered 2 parts of 5 equal parts. This situation is described by writing
.

Positive fraction
A number such as
is called a
positive fraction , or more simply, a
fraction .
The parts of a fraction
A fraction has
three parts .
- The fraction bar
.
Fraction bar
The
fraction bar serves as a grouping symbol. It separates a quantity into individual groups. These groups have names, as noted in 2 and 3 below.
- The nonzero number below the fraction bar.
Denominator
This number is called the
denominator of the fraction, and it indicates the number of parts the whole quantity has been divided into. Notice that the denominator must be a nonzero whole number since the least number of parts any quantity can have is one.
- The number above the fraction bar.
Numerator
This number is called the
numerator of the fraction, and it indicates how many of the specified parts are being considered. Notice that the numerator can be any whole number (including zero) since any number of the specified parts can be considered.
![]()






