| << Chapter < Page | Chapter >> Page > |
and then look for ways to relate this expression to expressions for rotational quantities. We note that , and we substitute this expression into , yielding
or
or
The moment of inertia of a long rod spun around an axis through one end perpendicular to its length is . Why is this moment of inertia greater than it would be if you spun a point mass at the location of the center of mass of the rod (at )? (That would be .)
Why is the moment of inertia of a hoop that has a mass and a radius greater than the moment of inertia of a disk that has the same mass and radius? Why is the moment of inertia of a spherical shell that has a mass and a radius greater than that of a solid sphere that has the same mass and radius?
Give an example in which a small force exerts a large torque. Give another example in which a large force exerts a small torque.
While reducing the mass of a racing bike, the greatest benefit is realized from reducing the mass of the tires and wheel rims. Why does this allow a racer to achieve greater accelerations than would an identical reduction in the mass of the bicycle’s frame?

A ball slides up a frictionless ramp. It is then rolled without slipping and with the same initial velocity up another frictionless ramp (with the same slope angle). In which case does it reach a greater height, and why?
Calculate the moment of inertia of a skater given the following information. (a) The 60.0-kg skater is approximated as a cylinder that has a 0.110-m radius. (b) The skater with arms extended is approximately a cylinder that is 52.5 kg, has a 0.110-m radius, and has two 0.900-m-long arms which are 3.75 kg each and extend straight out from the cylinder like rods rotated about their ends.
A soccer player extends her lower leg in a kicking motion by exerting a force with the muscle above the knee in the front of her leg. She produces an angular acceleration of and her lower leg has a moment of inertia of . What is the force exerted by the muscle if its effective perpendicular lever arm is 1.90 cm?
Suppose you exert a force of 180 N tangential to a 0.280-m-radius 75.0-kg grindstone (a solid disk).
(a)What torque is exerted? (b) What is the angular acceleration assuming negligible opposing friction? (c) What is the angular acceleration if there is an opposing frictional force of 20.0 N exerted 1.50 cm from the axis?
(a)
(b)
(c)
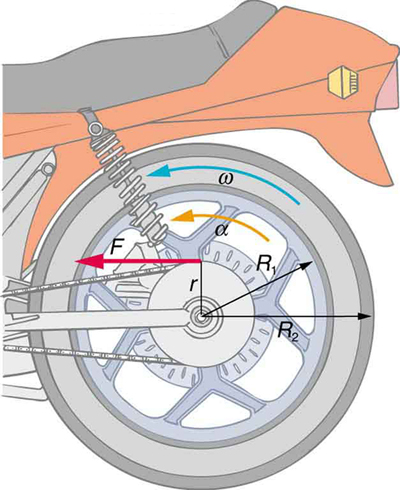
Consider the 12.0 kg motorcycle wheel shown in [link] . Assume it to be approximately an annular ring with an inner radius of 0.280 m and an outer radius of 0.330 m. The motorcycle is on its center stand, so that the wheel can spin freely. (a) If the drive chain exerts a force of 2200 N at a radius of 5.00 cm, what is the angular acceleration of the wheel? (b) What is the tangential acceleration of a point on the outer edge of the tire? (c) How long, starting from rest, does it take to reach an angular velocity of 80.0 rad/s?
Zorch, an archenemy of Superman, decides to slow Earth’s rotation to once per 28.0 h by exerting an opposing force at and parallel to the equator. Superman is not immediately concerned, because he knows Zorch can only exert a force of (a little greater than a Saturn V rocket’s thrust). How long must Zorch push with this force to accomplish his goal? (This period gives Superman time to devote to other villains.) Explicitly show how you follow the steps found in Problem-Solving Strategy for Rotational Dynamics .
or
An automobile engine can produce 200 N ∙ m of torque. Calculate the angular acceleration produced if 95.0% of this torque is applied to the drive shaft, axle, and rear wheels of a car, given the following information. The car is suspended so that the wheels can turn freely. Each wheel acts like a 15.0 kg disk that has a 0.180 m radius. The walls of each tire act like a 2.00-kg annular ring that has inside radius of 0.180 m and outside radius of 0.320 m. The tread of each tire acts like a 10.0-kg hoop of radius 0.330 m. The 14.0-kg axle acts like a rod that has a 2.00-cm radius. The 30.0-kg drive shaft acts like a rod that has a 3.20-cm radius.

Notification Switch
Would you like to follow the 'Unit 8 - rotational motion' conversation and receive update notifications?