2.6 Moments and centers of mass  (Page 7/14)

Theorem of pappus

This section ends with a discussion of the theorem of Pappus for volume    , which allows us to find the volume of particular kinds of solids by using the centroid. (There is also a theorem of Pappus for surface area, but it is much less useful than the theorem for volume.)

Proof

We can prove the case when the region is bounded above by the graph of a function $f(x)$ and below by the graph of a function $g(x)$ over an interval $\left[a,b\right],$ and for which the axis of revolution is the y -axis. In this case, the area of the region is $A={{\displaystyle \int }}_a^b\left[f(x)-g(x)\right]dx.$ Since the axis of rotation is the y -axis, the distance traveled by the centroid of the region depends only on the x -coordinate of the centroid, $\bar{x},$ which is

where

Then,

and thus

However, using the method of cylindrical shells, we have

So,

and the proof is complete.

□

Using the theorem of pappus for volume

Let R be a circle of radius 2 centered at $\left(4,0\right).$ Use the theorem of Pappus for volume to find the volume of the torus generated by revolving R around the y -axis.

The region and torus are depicted in the following figure.

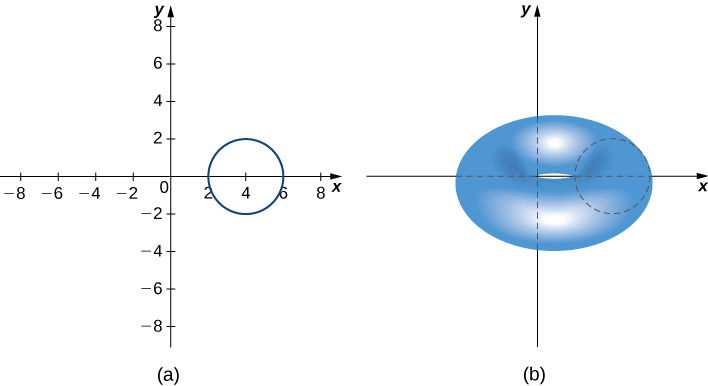
The region R is a circle of radius 2, so the area of R is $A=4\pi$ units ² . By the symmetry principle, the centroid of R is the center of the circle. The centroid travels around the y -axis in a circular path of radius 4, so the centroid travels $d=8\pi$ units. Then, the volume of the torus is $A·d=32{\pi }^2$ units ³ .

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Key concepts

• Mathematically, the center of mass of a system is the point at which the total mass of the system could be concentrated without changing the moment. Loosely speaking, the center of mass can be thought of as the balancing point of the system.
• For point masses distributed along a number line, the moment of the system with respect to the origin is $M={\displaystyle \sum }_{i=1}^n{m}_i{x}_i.$ For point masses distributed in a plane, the moments of the system with respect to the x - and y -axes, respectively, are $M_x={\displaystyle \sum }_{i=1}^n{m}_i{y}_i$ and $M_y={\displaystyle \sum }_{i=1}^n{m}_i{x}_i,$ respectively.
• For a lamina bounded above by a function $f(x),$ the moments of the system with respect to the x - and y -axes, respectively, are $M_x=\rho {\displaystyle {\int }_a^b\frac{{\left[f(x)\right]}^2}{2}dx}$ and $M_y=\rho {\displaystyle {\int }_a^{b}xf(x)dx}.$
• The x - and y -coordinates of the center of mass can be found by dividing the moments around the y -axis and around the x -axis, respectively, by the total mass. The symmetry principle says that if a region is symmetric with respect to a line, then the centroid of the region lies on the line.
• The theorem of Pappus for volume says that if a region is revolved around an external axis, the volume of the resulting solid is equal to the area of the region multiplied by the distance traveled by the centroid of the region.