| << Chapter < Page | Chapter >> Page > |
For the following exercises, calculate the center of mass for the collection of masses given.
at and at
at and at
For the following exercises, compute the center of mass
for and for
For the following exercises, compute the center of mass Use symmetry to help locate the center of mass whenever possible.
in the square
for the region bounded by and
For the following exercises, use a calculator to draw the region, then compute the center of mass Use symmetry to help locate the center of mass whenever possible.
[T] The region between and
[T] Region between and
[T] The region bounded by and
For the following exercises, use the theorem of Pappus to determine the volume of the shape.
Rotating around the -axis between and
A general cone created by rotating a triangle with vertices and around the -axis. Does your answer agree with the volume of a cone?
A general cylinder created by rotating a rectangle with vertices and around the -axis. Does your answer agree with the volume of a cylinder?
A sphere created by rotating a semicircle with radius around the -axis. Does your answer agree with the volume of a sphere?
For the following exercises, use a calculator to draw the region enclosed by the curve. Find the area and the centroid for the given shapes. Use symmetry to help locate the center of mass whenever possible.
[T] Triangle: and
[T] Ring: and
Find the generalized center of mass in the sliver between and with Then, use the Pappus theorem to find the volume of the solid generated when revolving around the y -axis.
Find the generalized center of mass between and Then, use the Pappus theorem to find the volume of the solid generated when revolving around the y -axis.
Center of mass: volume:
Find the generalized center of mass between and Then, use the Pappus theorem to find the volume of the solid generated when revolving around the y -axis.
Use the theorem of Pappus to find the volume of a torus (pictured here). Assume that a disk of radius is positioned with the left end of the circle at and is rotated around the y -axis.
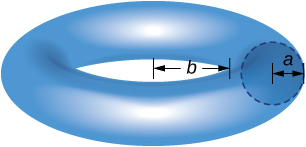
Volume:
Find the center of mass for a thin wire along the semicircle with unit mass. ( Hint: Use the theorem of Pappus.)

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?