| << Chapter < Page | Chapter >> Page > |
Let R be the region bounded above by the graph of the function and below by the graph of the function Find the centroid of the region.
The centroid of the region is
We stated the symmetry principle earlier, when we were looking at the centroid of a rectangle. The symmetry principle can be a great help when finding centroids of regions that are symmetric. Consider the following example.
Let R be the region bounded above by the graph of the function and below by the x -axis. Find the centroid of the region.
The region is depicted in the following figure.
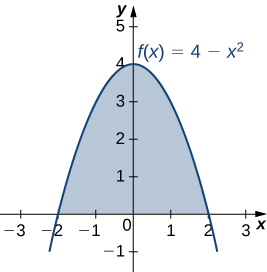
The region is symmetric with respect to the y -axis. Therefore, the x -coordinate of the centroid is zero. We need only calculate Once again, for the sake of convenience, assume
First, we calculate the total mass:
Next, we calculate the moments. We only need
Then we have
The centroid of the region is
Let R be the region bounded above by the graph of the function and below by x -axis. Find the centroid of the region.
The centroid of the region is
The Grand Canyon Skywalk opened to the public on March 28, 2007. This engineering marvel is a horseshoe-shaped observation platform suspended 4000 ft above the Colorado River on the West Rim of the Grand Canyon. Its crystal-clear glass floor allows stunning views of the canyon below (see the following figure).

The Skywalk is a cantilever design, meaning that the observation platform extends over the rim of the canyon, with no visible means of support below it. Despite the lack of visible support posts or struts, cantilever structures are engineered to be very stable and the Skywalk is no exception. The observation platform is attached firmly to support posts that extend 46 ft down into bedrock. The structure was built to withstand 100-mph winds and an 8.0-magnitude earthquake within 50 mi, and is capable of supporting more than 70,000,000 lb.
One factor affecting the stability of the Skywalk is the center of gravity of the structure. We are going to calculate the center of gravity of the Skywalk, and examine how the center of gravity changes when tourists walk out onto the observation platform.
The observation platform is U-shaped. The legs of the U are 10 ft wide and begin on land, under the visitors’ center, 48 ft from the edge of the canyon. The platform extends 70 ft over the edge of the canyon.
To calculate the center of mass of the structure, we treat it as a lamina and use a two-dimensional region in the xy -plane to represent the platform. We begin by dividing the region into three subregions so we can consider each subregion separately. The first region, denoted consists of the curved part of the U. We model as a semicircular annulus, with inner radius 25 ft and outer radius 35 ft, centered at the origin (see the following figure).
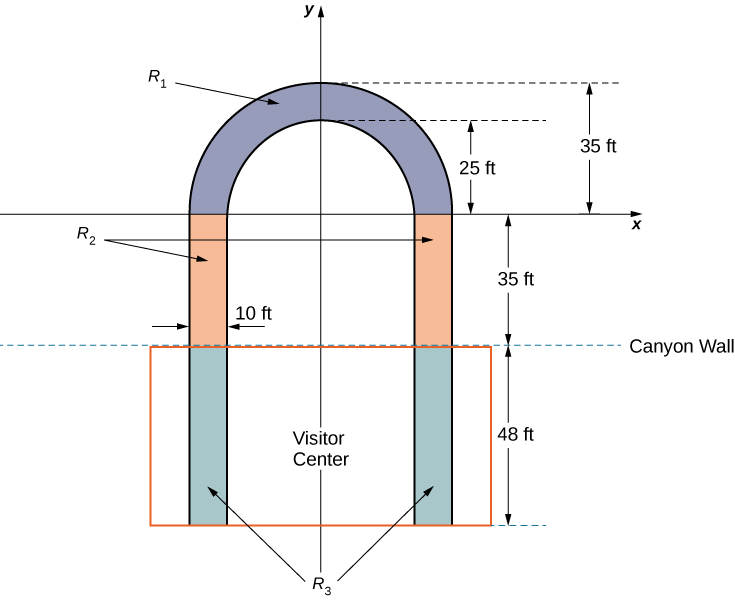
The legs of the platform, extending 35 ft between and the canyon wall, comprise the second sub-region, Last, the ends of the legs, which extend 48 ft under the visitor center, comprise the third sub-region, Assume the density of the lamina is constant and assume the total weight of the platform is 1,200,000 lb (not including the weight of the visitor center; we will consider that later). Use

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?