| << Chapter < Page | Chapter >> Page > |
Notice that the expression for is replaced by when working in polar coordinates. Another way to look at the polar double integral is to change the double integral in rectangular coordinates by substitution. When the function is given in terms of and using changes it to
Note that all the properties listed in Double Integrals over Rectangular Regions for the double integral in rectangular coordinates hold true for the double integral in polar coordinates as well, so we can use them without hesitation.
Sketch the polar rectangular region
As we can see from [link] , and are circles of radius and covers the entire top half of the plane. Hence the region looks like a semicircular band.
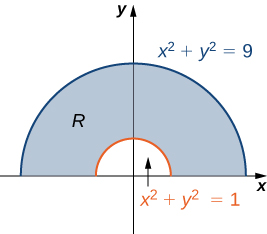
Now that we have sketched a polar rectangular region, let us demonstrate how to evaluate a double integral over this region by using polar coordinates.
Evaluate the integral over the region
First we sketch a figure similar to [link] but with outer radius From the figure we can see that we have
Evaluate the integral where is the unit circle on the -plane.
The region is a unit circle, so we can describe it as
Using the conversion and we have
Evaluate the integral where
We can see that is an annular region that can be converted to polar coordinates and described as (see the following graph).
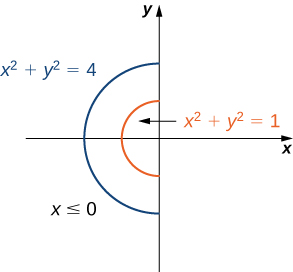
Hence, using the conversion and we have
Evaluate the integral where is the circle of radius on the -plane.
To evaluate the double integral of a continuous function by iterated integrals over general polar regions, we consider two types of regions, analogous to Type I and Type II as discussed for rectangular coordinates in Double Integrals over General Regions . It is more common to write polar equations as than so we describe a general polar region as (see the following figure).
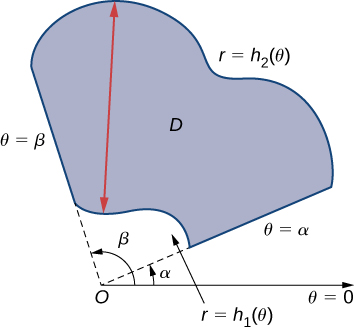
If is continuous on a general polar region as described above, then

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?