| << Chapter < Page | Chapter >> Page > |
Professor Price has a weakness for cream filled donuts, but he believes that some bakeries are not properly filling the donuts. A sample of 24 donuts reveals a meanamount of filling equal to 0.5 cups, and the sample standard deviation is 0.11 cups. Professor Price has an interest in the average quantity of filling, of course, but he isparticularly distressed if one donut is radically different from another. Professor Price does not like surprises.
Test at 5% the null that the population variance of donut filling is significantly different from the average amount of filling.
This is clearly a problem dealing with variances. In this case we are testing a single sample rather than comparing two samples from different populations. The null and alternative hypotheses are thus:
The FCC conducts broadband speed tests to measure how much data per second passes between a consumer’s computer and the internet. As of August of 2012, the standard deviation of Internet speeds across Internet Service Providers (ISPs) was 12.2 percent. Suppose a sample of 15 ISPs is taken, and the standard deviation is 13.2. An analyst claims that the standard deviation of speeds is more than what was reported. State the null and alternative hypotheses, compute the degrees of freedom, the test statistic, sketch the graph of the distribution and mark the area associated with the level of confidence, and draw a conclusion. Test at the 1% significance level.
H 0 : σ 2 = 12.2 2
H
a :
σ
2 >12.2
2
df = 14
chi
2 test statistic = 16.39
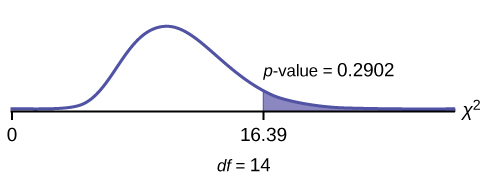
The p -value is 0.2902, so we decline to reject the null hypothesis. There is not enough evidence to suggest that the variance is greater than 12.2 2 .
In
2nd DISTR , use7:
χ2cdf . The syntax is
(lower, upper, df) for the parameter list.
χ2cdf(16.39,10^99,14) . The
p -value = 0.2902.
“AppleInsider Price Guides.” Apple Insider, 2013. Available online at http://appleinsider.com/mac_price_guide (accessed May 14, 2013).
Data from the World Bank, June 5, 2012.
To test variability, use the chi-square test of a single variance. The test may be left-, right-, or two-tailed, and its hypotheses are always expressed in terms of the variance (or standard deviation).
Test of a single variance statistic where:
n : sample size
s : sample standard deviation
: hypothesized value of the population standard deviation
df = n – 1 Degrees of freedom
Use the following information to answer the next three exercises: An archer’s standard deviation for his hits is six (data is measured in distance from the center of the target). An observer claims the standard deviation is less.
What type of test should be used?
a test of a single variance
State the null and alternative hypotheses.
Is this a right-tailed, left-tailed, or two-tailed test?
a left-tailed test
Use the following information to answer the next three exercises: The standard deviation of heights for students in a school is 0.81. A random sample of 50 students is taken, and the standard deviation of heights of the sample is 0.96. A researcher in charge of the study believes the standard deviation of heights for the school is greater than 0.81.
What type of test should be used?
State the null and alternative hypotheses.
H 0 : σ 2 = 0.81 2 ;
H a : σ 2 >0.81 2
df = ________
Use the following information to answer the next four exercises: The average waiting time in a doctor’s office varies. The standard deviation of waiting times in a doctor’s office is 3.4 minutes. A random sample of 30 patients in the doctor’s office has a standard deviation of waiting times of 4.1 minutes. One doctor believes the variance of waiting times is greater than originally thought.
What type of test should be used?
a test of a single variance
What is the test statistic?
What can you conclude at the 5% significance level?

Notification Switch
Would you like to follow the 'Introductory statistics' conversation and receive update notifications?