| << Chapter < Page | Chapter >> Page > |
. Find the cross product.
This means that , or, 5 is to 4 as 20 is to 6.
Find the cross product.
The means that , or, 16 is to 3 as 64 is to 12.
Find the unknown number in each proportion.
Recall that a rate is a comparison, by division, of unlike denominate numbers. We must be careful when setting up proportions that involve rates. The form is important. For example, if a rate involves two types of units, say unit type 1 and unit type 2, we can write
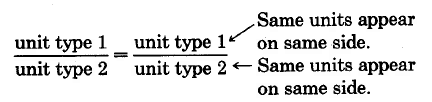
or

Both cross products produce a statement of the type
which we take to mean the comparison

Examples of correctly expressed proportions are the following:
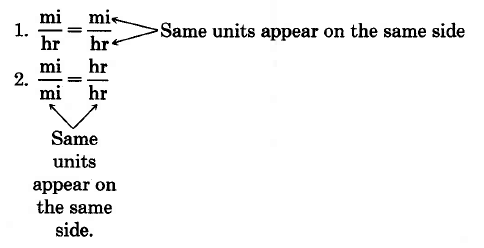
However, if we write the same type of units on different sides, such as,
the cross product produces a statement of the form

We can see that this is an incorrect comparison by observing the following example: It is incorrect to write
for two reason.
A statement that two ratios or
rates, proportion
For the following 9 problems, write each proportion in fractional form.
3 is to 7 as 18 is to 42.
9 is to 14 as 27 is to 42.
5 liters is to 1 bottle as 20 liters is to 4 bottles.
18 grams of cobalt is to 10 grams of silver as 36 grams of cobalt is to 20 grams of silver.
4 cups of water is to 1 cup of sugar as 32 cups of water is to 8 cups of sugar.
3 people absent is to 31 people present as 15 people absent is to 155 people present.
6 dollars is to 1 hour as 90 dollars is to 15 hours.
For the following 10 problems, write each proportion as a sentence.
For the following 10 problems, solve each proportion.
For the following 5 problems, express each sentence as a proportion then solve the proportion.
cushions are to 2 sofas as 24 cushions are to 16 sofas.
1 spacecraft is to 7 astronauts as 5 spacecraft are to astronauts.
56 microchips are to x circuit boards as 168 microchips are to 3 circuit boards.
18 calculators are to 90 calculators as students are to 150 students.
dollars are to $40,000 as 2 sacks are to 1 sack.
Indicate whether the proportion is true or false.
( [link] ) Use the number 5 and 7 to illustrate the commutative property of addition.
( [link] ) Use the numbers 5 and 7 to illustrate the commutative property of multiplication.
( [link] ) Find the product. .
( [link] ) Write the simplified fractional form of the rate “sixteen sentences to two paragraphs.”

Notification Switch
Would you like to follow the 'Fundamentals of mathematics' conversation and receive update notifications?