| << Chapter < Page | Chapter >> Page > |
Para la recepción, tomaremos el vector Y. Cualquier error de transmisión resultará en Y≠X. Uno de los métodos más fáciles es haciendo uso de una matriz de chequeo de paridad H derivada de la sub-matriz P. Se define como:

Si esta última condición no se cumple, el código recibido contiene errores. La detección de errores puede basarse a partir del vector síndrome S:
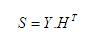
Si todos los elementos de S son iguales a CERO, entonces hay dos posibilidades:
De igual forma, los errores se indican con la presencia de elementos distintos a cero en S.
Ahora bien, si el vector X se corrompe con un vector de error E, el vector Y resultará en:
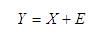
Por lo que S será:
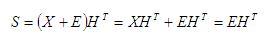
Esto evidencia que el Síndrome dependerá completamente del patrón de error, no del vector transmitido. Al existir errores en la codificación, S indicará en dónde se encuentra el mismo.
Si un código debe corregir hasta t errores por palabra, entonces q y n deben cumplir con la desigualdad o relación de Hamming, definida como:
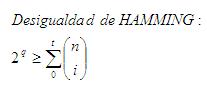
Es un código de bloques lineal (n,k) con 3 ó más bits de chequeo/redundancia (q) que cumple con estas ecuaciones:
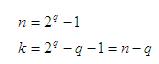
Dado que su distancia mínima siempre es 3 (sin importar el valor de q), este tipo de código es capaz de corregir hasta un error y detectar dos, por lo que:
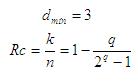
Supongamos el caso Hamming (7,4) (n=7, q=3, k=4). Para construir dicho código, tomamos la sub-matriz P de la matriz generadora G y la llenamos con todas las palabras de q bits que tengan dos o más 1’s, sin ningún orden en particular. Como son k=4 bits de mensaje original, entonces la matriz G tendrá cuatro filas. Entonces:

Dado un bloque de bits de mensaje M = (m 1 m 2 m 3 m 4 ), los bits de chequeo se calculan sustituyendo los elementos de la sub-matriz P en la ecuación C=MP, por lo que:
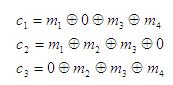
Para este ejemplo se pudiera construir un codificador Hamming de la siguiente forma:
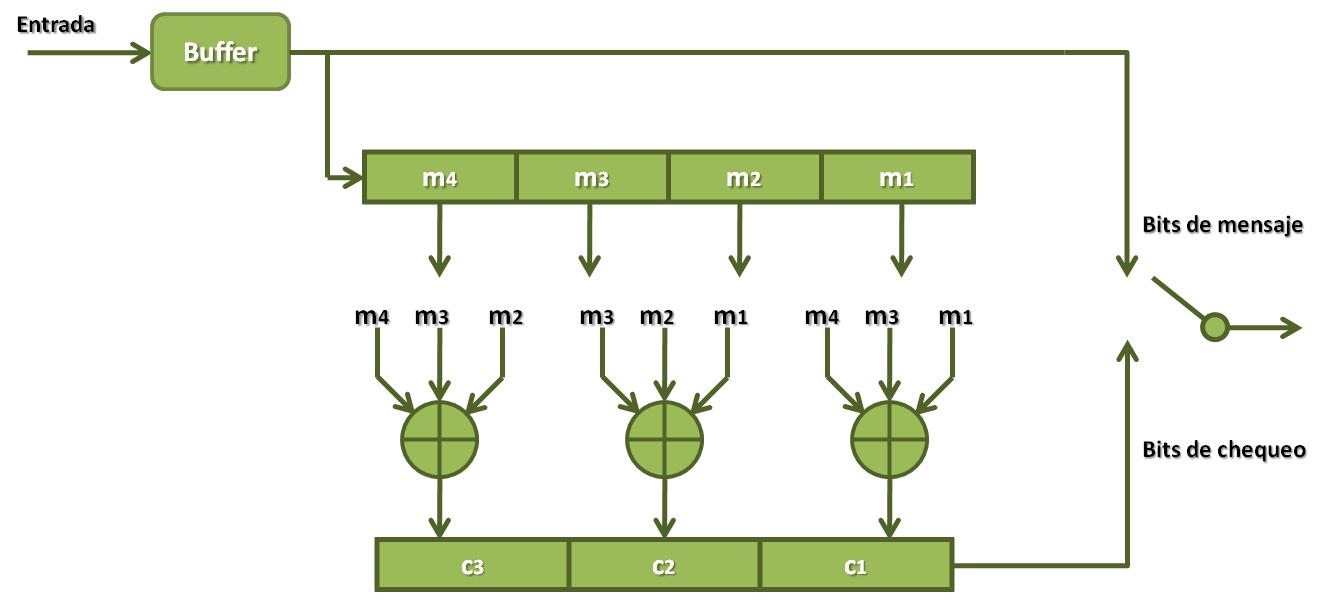
Las palabras código correspondientes a este código Hamming (7,4) se observan en la tabla (Todas generadas a partir de C=MP):
| Mensaje | Bits Redundantes | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
A diferencia de la codificación por bloque, los códigos convolucionales trabajan bit por bit. Su estructura pudiera generalizarse de la siguiente forma:
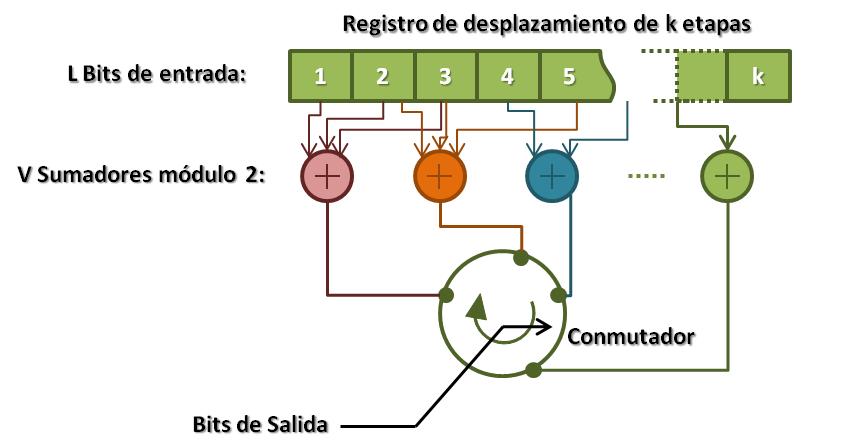
Esta estructura genera V símbolos a la salida por cada símbolo de entrada. Su tasa de símbolos de salida será entonces Rc=1/V. Existen 4 métodos de representación de los códigos convolucionales:
Supongamos que se tiene el siguiente codificador convolucional:
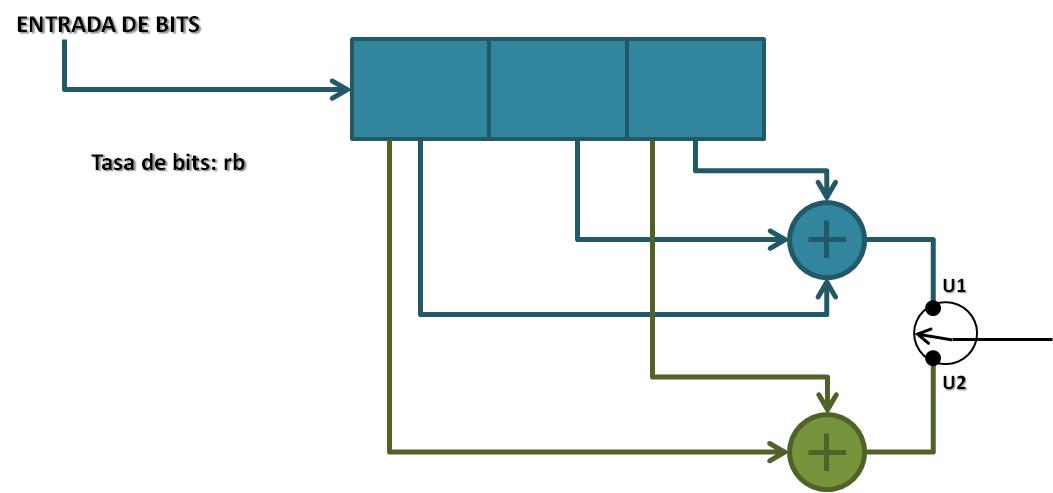
Para que el código funcione correctamente, antes de que llegue el primer bit del mensaje el registro de desplazamiento está ‘limpio’ (Sólo contiene 0’s). Esto implica que la primera salida será U1=0 y U2=0. Supongamos que el mensaje de entrada es 101 . Entonces, el codificador hará los siguientes pasos:
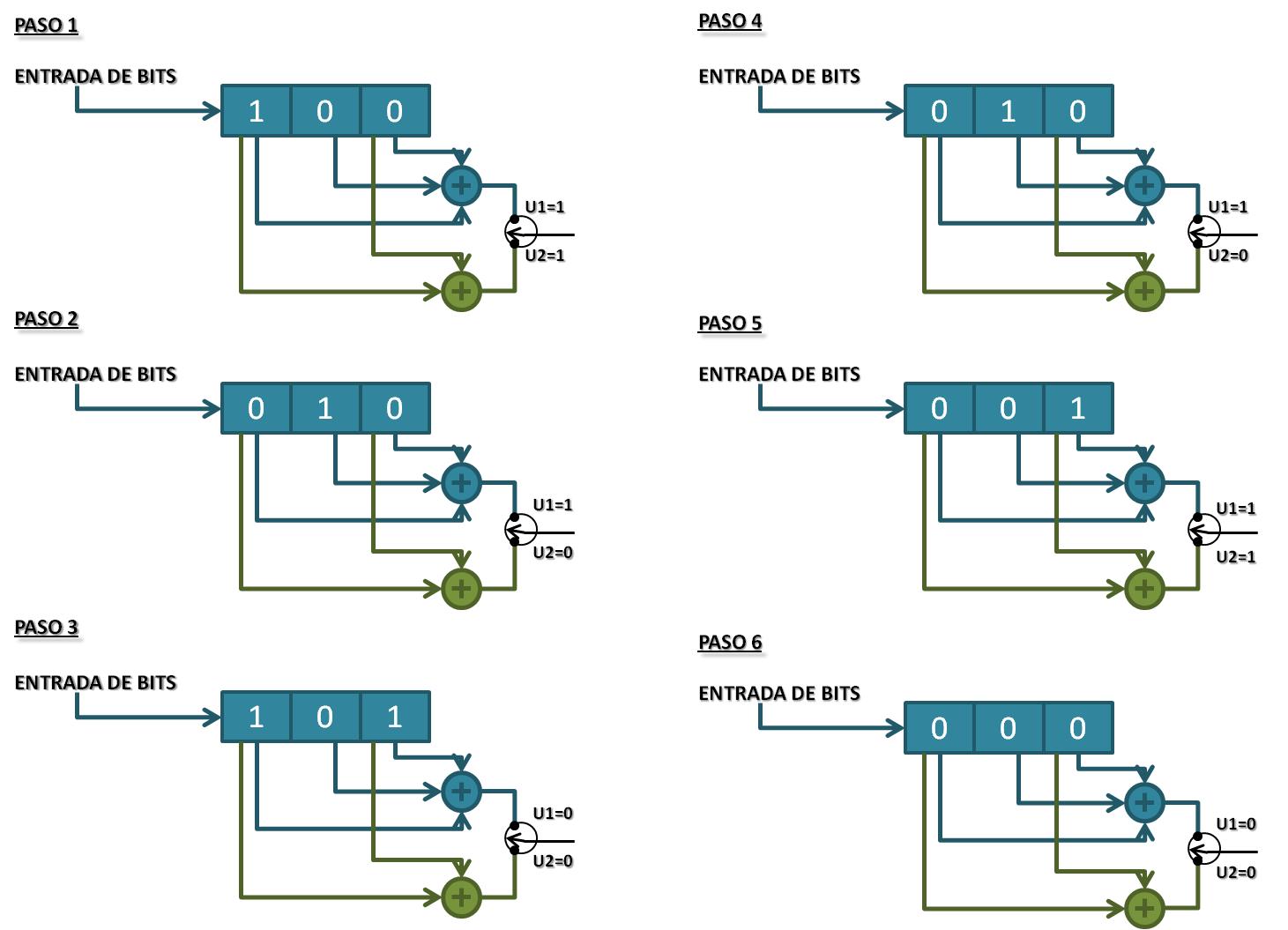
La secuencia de salida será:
| U1 | U2 |
| 1 | 1 |
| 1 | 0 |
| 0 | 0 |
| 1 | 0 |
| 1 | 1 |
El estado del codificador convolucional se define como los contenidos de los registros de desplazamiento de las k-1 etapas más a la derecha del codificador. Para el ejemplo actual:
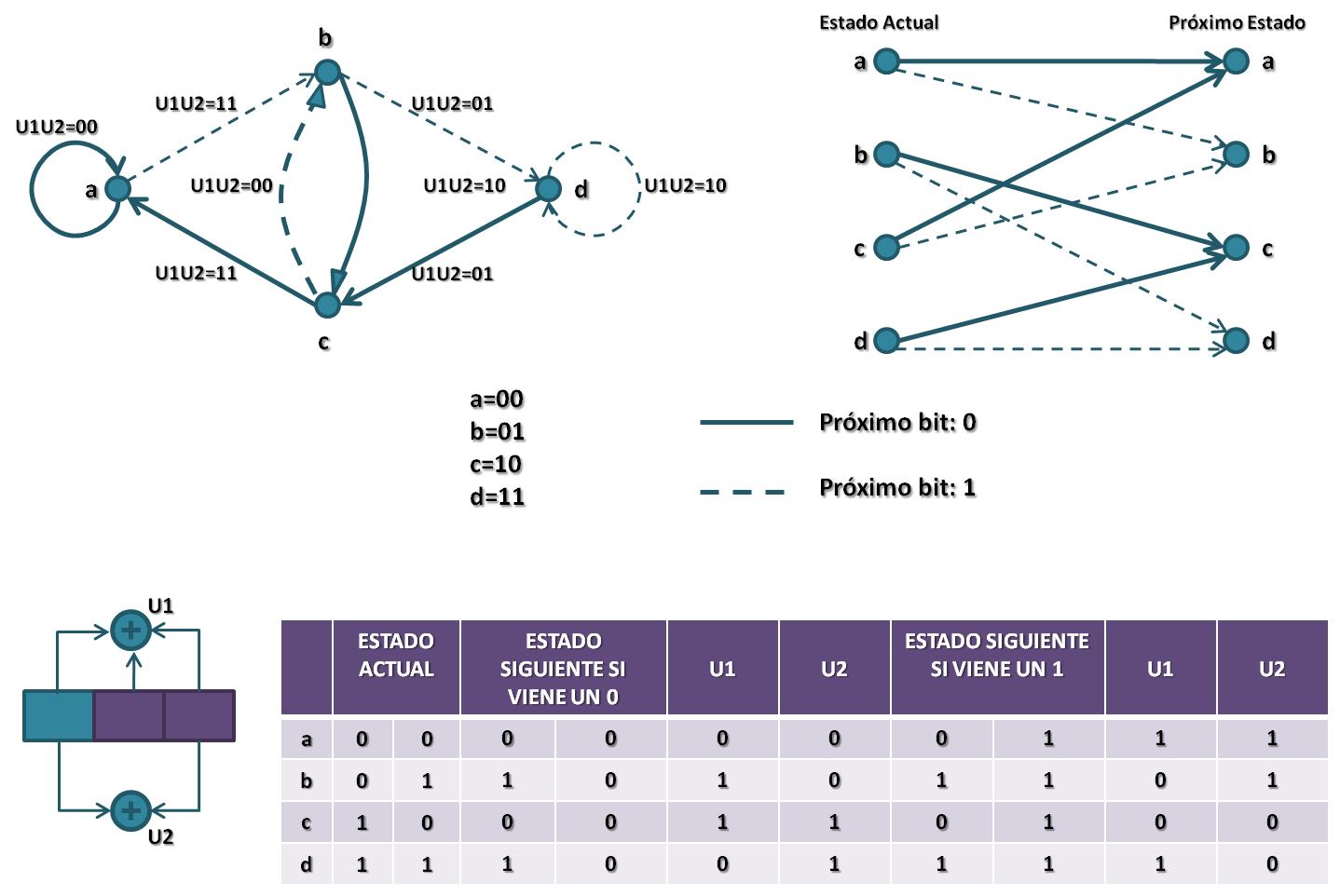
La raíz representa el estado inicial (U1U2=00). Si el próximo bit es un 0, se toma la ramificación superior. Dado que la longitud del registro es igual a 3 (L=3), entonces el árbol será:

A través de él se puede observar la evolución del codificador por cada T que pase. El diagrama deberá tener 2 k-1 nodos que representen los posibles estados (a,b,c y d). Entonces:
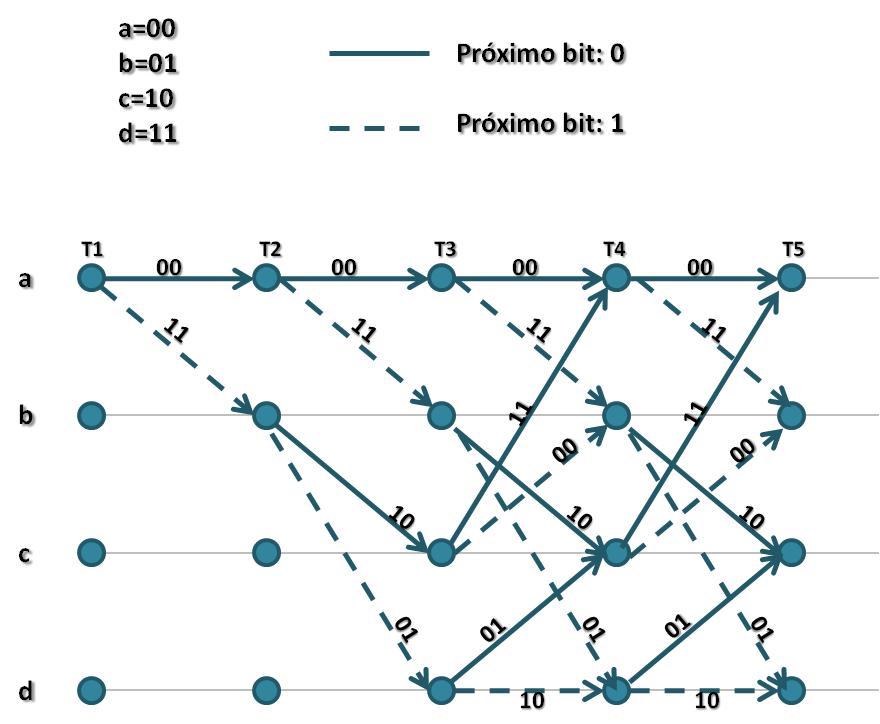
Para la decodificación implementamos la
máxima verosimilitud (

Esto puede verse a través del Algoritmo de Viterbi : Se basa en el Diagrama de Trellis. Asigna a cada rama una métrica que es igual a la distancia Hamming correspondiente a la rama recibida y todas las ramas de Trellis que intervienen en ese instante de tiempo. Supongamos el siguiente ejemplo:
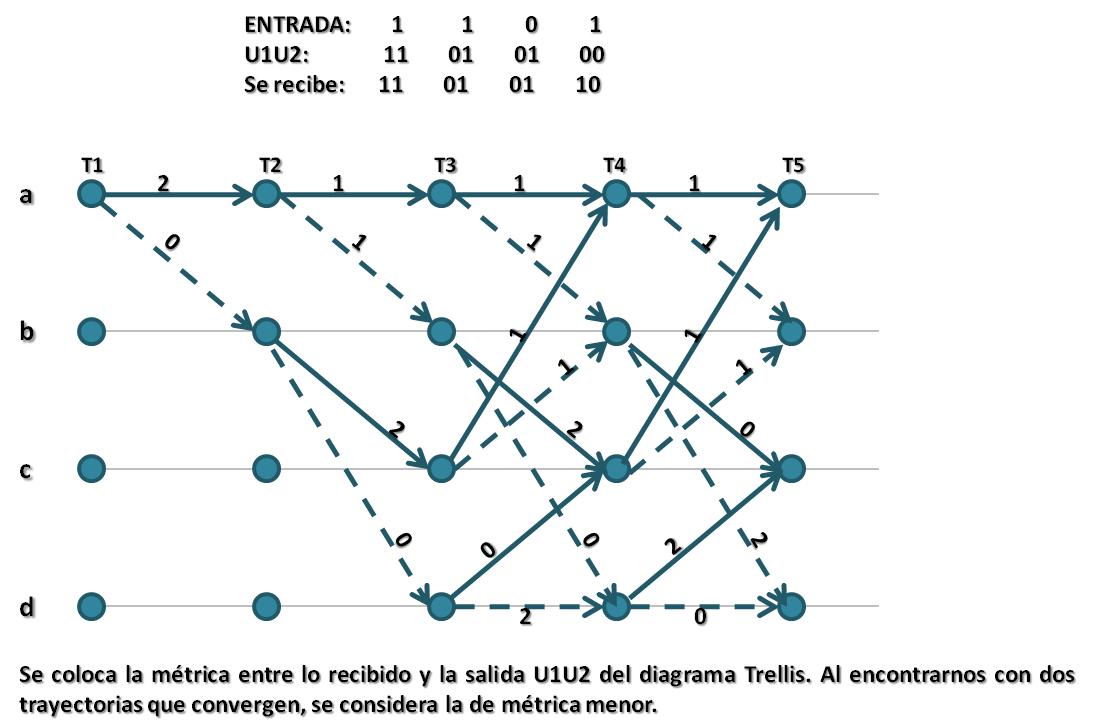
Como se observa, se debe esperar hasta el instante T4 (que es cuando empiezan a cerrarse los lazos) para tomar una decisión sobre el camino más corto. Allí, se tendrán dos caminos para llegar a ese instante:

Partiendo del estado a, en el estado 4 convergen dos trayectorias dos métricas: la primera con un total de 4(la de arriba) y la segunda con un total de 3(la que va por debajo). Luego se analizan situaciones similares en T4. Por ejemplo, al estado b en T4 se llega por dos trayectorias: la de arriba con métrica 4 y la de abajo con métrica 3. Para T4 pero al estado c también se llega por dos caminos: el de arriba con métrica 5 y el de abajo con métrica 0. Para T4 pero al estado d los dos caminos tienen métricas 3 y 2 respectivamente. Al eliminar todas las trayectorias de métrica mayor, en este ejemplo se logra ya despejar el bit transmitido entre la transición T1-T2 y decidir que es un “1”.
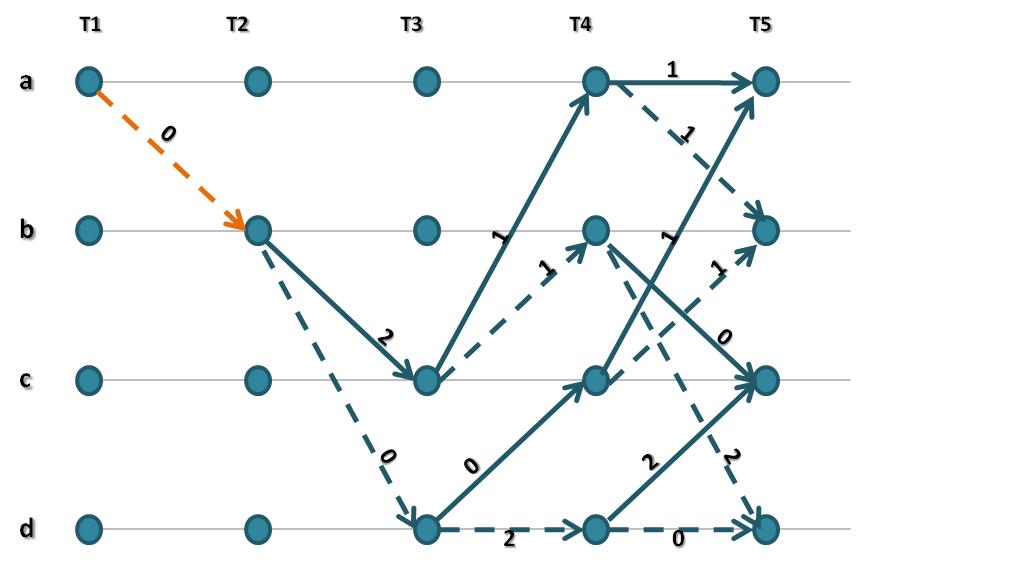
Se repite el mismo procedimiento para el nodo T5 y luego para los demás nodos hasta que se vayan obteniendo cada uno de los bits transmitidos.
Se descartan entonces todos los caminos no viables. Este proceso debe repetirse hasta que se logre obtener la secuencia original.
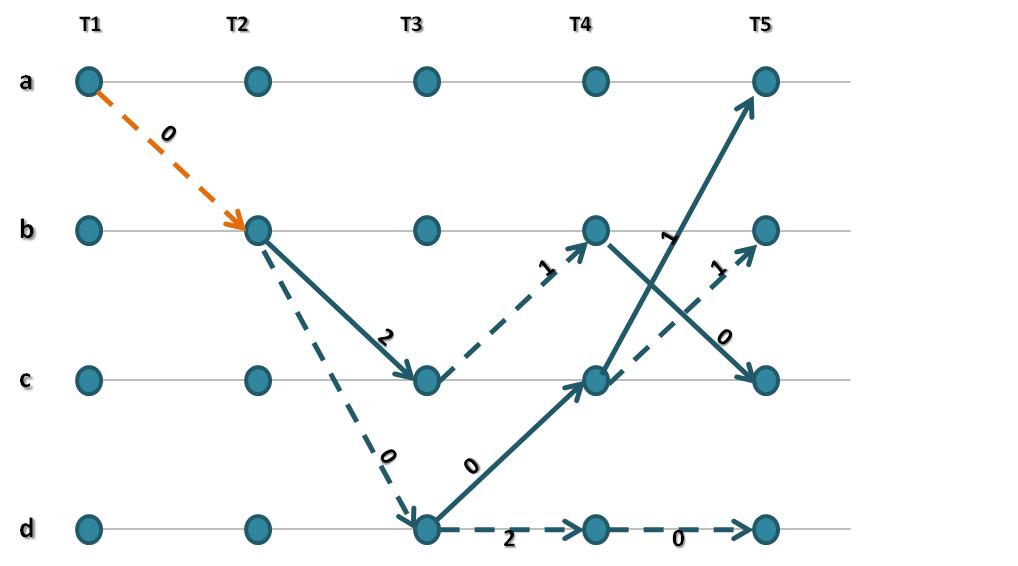
Las pruebas para las codificaciones Hamming(7,4), Hamming(15,11) y Convolucional pueden realizarse descargando el VI del siguiente enlace:

Notification Switch
Would you like to follow the 'Laboratorio digital interactivo' conversation and receive update notifications?