0.8 Exponential functions and graphs  (Page 2/2)

Therefore, if $a<0$ , then the range is $(-\infty ,q)$ , meaning that $f\left(x\right)$ can be any real number less than $q$ . Equivalently, one could write that the range is $\{y\in \mathbb{R}:y<q\}$ .

For example, the domain of $g\left(x\right)=3·2^{x+1}+2$ is $\{x:x\in \mathbb{R}\}$ . For the range,

Therefore the range is $\left\{g\right(x):g(x)\in [2,\infty \left)\right\}$ .

Domain and range

1. Give the domain of $y=3^x$ .
2. What is the domain and range of $f\left(x\right)=2^x$ ?
3. Determine the domain and range of $y={(1,5)}^{x+3}$ .

Intercepts

For functions of the form, $y=a{b}^{(x+p)}+q$ , the intercepts with the $x$ - and $y$ -axis are calculated by setting $x=0$ for the $y$ -intercept and by setting $y=0$ for the $x$ -intercept.

The $y$ -intercept is calculated as follows:

For example, the $y$ -intercept of $g\left(x\right)=3·2^{x+1}+2$ is given by setting $x=0$ to get:

The $x$ -intercepts are calculated by setting $y=0$ as follows:

Since $b>0$ (this is a requirement in the original definition) and a positive number raised to any power is always positive, the last equation above only has a real solution if either $a<0$ or $q<0$ (but not both). Additionally, $a$ must not be zero for the division to be valid. If these conditions are not satisfied, the graph of the function of the form $y=a{b}^{(x+p)}+q$ does not have any $x$ -intercepts.

For example, the $x$ -intercept of $g\left(x\right)=3·2^{x+1}+2$ is given by setting $y=0$ to get:

which has no real solution. Therefore, the graph of $g\left(x\right)=3·2^{x+1}+2$ does not have a $x$ -intercept. You will notice that calculating $g\left(x\right)$ for any value of $x$ will always give a positive number, meaning that $y$ will never be zero and so the graph will never intersect the $x$ -axis.

Intercepts

1. Give the y-intercept of the graph of $y=b^x+2$ .
2. Give the x- and y-intercepts of the graph of $y=\frac{1}{2}{(1,5)}^{x+3}-0,75$ .

Asymptotes

Functions of the form $y=a{b}^{(x+p)}+q$ always have exactly one horizontal asymptote.

When examining the range of these functions, we saw that we always have either $y<q$ or $y>q$ for all input values of $x$ . Therefore the line $y=q$ is an asymptote.

For example, we saw earlier that the range of $g\left(x\right)=3·2^{x+1}+2$ is $(2,\infty )$ because $g\left(x\right)$ is always greater than 2. However, the value of $g\left(x\right)$ can get extremely close to 2, even though it never reaches it. For example, if you calculate $g(-20)$ , the value is approximately 2.000006. Using larger negative values of $x$ will make $g\left(x\right)$ even closer to 2: the value of $g(-100)$ is so close to 2 that the calculator is not precise enough to know the difference, and will (incorrectly) show you that it is equal to exactly 2.

From this we deduce that the line $y=2$ is an asymptote.

Asymptotes

1. Give the equation of the asymptote of the graph of $y=3^x-2$ .
2. What is the equation of the horizontal asymptote of the graph of $y=3{(0,8)}^{x-1}-3$ ?

Sketching graphs of the form $f\left(x\right)=a{b}^{(x+p)}+q$

In order to sketch graphs of functions of the form, $f\left(x\right)=a{b}^{(x+p)}+q$ , we need to determine four characteristics:

1. domain and range
2. $y$ -intercept
3. $x$ -intercept

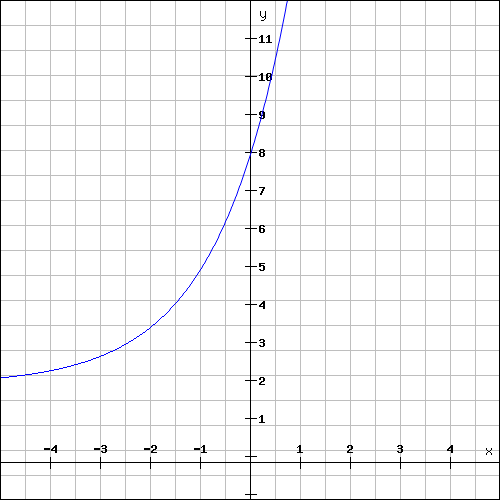
For example, sketch the graph of $g\left(x\right)=3·2^{x+1}+2$ . Mark the intercepts.

We have determined the domain to be $\{x:x\in \mathbb{R}\}$ and the range to be $\left\{g\right(x):g(x)\in (2,\infty \left)\right\}$ .

The $y$ -intercept is $y_{int}=8$ and there is no $x$ -intercept.

Sketching graphs

1. Draw the graphs of the following on the same set of axes. Label the horizontal asymptotes and y-intercepts clearly.
   1. $y=b^x+2$
   2. $y=b^{x+2}$
   3. $y=2b^x$
   4. $y=2b^{x+2}+2$
   1. Draw the graph of $f\left(x\right)=3^x$ .
   2. Explain where a solution of $3^x=5$ can be read off the graph.

End of chapter exercises

1. The following table of values has columns giving the $y$ -values for the graph $y=a^x$ , $y=a^{x+1}$ and $y=a^x+1$ . Match a graph to a column.

   $x$	A	B	C
   -2	7,25	6,25	2,5
   -1	3,5	2,5	1
   0	2	1	0,4
   1	1,4	0,4	0,16
   2	1,16	0,16	0,064

2. The graph of $f\left(x\right)=1+a.2^x$ (a is a constant) passes through the origin.
   1. Determine the value of $a$ .
   2. Determine the value of $f(-15)$ correct to FIVE decimal places.
   3. Determine the value of $x$ , if $P(x;0,5)$ lies on the graph of $f$ .
   4. If the graph of $f$ is shifted 2 units to the right to give the function $h$ , write down the equation of $h$ .
3. The graph of $f\left(x\right)=a.b^x(a\ne 0)$ has the point P(2;144) on $f$ .
   1. If $b=0,75$ , calculate the value of $a$ .
   2. Hence write down the equation of $f$ .
   3. Determine, correct to TWO decimal places, the value of $f\left(13\right)$ .
   4. Describe the transformation of the curve of $f$ to $h$ if $h\left(x\right)=f(-x)$ .