| << Chapter < Page | Chapter >> Page > |
The expressions in the brackets are constant. Let,
Substituting in the expression of displacement, we have :
Following standard analytical method, Let
Substituting in the expression of displacement again, we have :
This is the final expression of the composition of two SHMs in the same straight line. Clearly, the amplitude of resulting SHM is “A”. Also, the resulting SHM differs in phase with respect to either of the two SHMs. In particular, the phase of resulting SHM differs by an angle “θ” with respect of first SHM, whose displacement is given by “ ” We also note that frequency of the resulting SHM is same as either of two SHMs.
The phase constant of the resulting SHM is :
The amplitude of the resultant harmonic motion is obtained solving substitutions made in the derivation.
We ,here, consider few interesting cases :
Two SHMs are in same phase. In this case, .
If additionally , then . Further, phase constant is given by :
Two SHMs are opposite in phase. In this case, .
The amplitude is a non-negative number. In order to reflect this aspect, we write amplitude in modulus form :
If additionally , then A = 0. In this case, the particle does not oscillate. Further, phase constant is given by :
We have evaluated composition of two SHMs analytically. This has given us the detailed picture of how displacement of a particle takes place. In the nutshell, we find that resulting motion is also a SHM of same frequency as that of constituting SHMs. Besides, we are able to determine followings aspects of resulting SHM :
There is, however, an effective and more convenient alternative to determine all these aspects of SHM, using vector concept. The important thing to realize here is that amplitude can be associated with direction – apart from having magnitude. Its direction is qualified by the phase constant.
The equation of amplitude, derived earlier, provides the basis of this assumption. If we look closely at the expression of resultant amplitude, then we realize that the expression actually represents sum of two vectors namely “ ” and “ ” at an angle “φ” as shown in the figure.
Composition of two shms
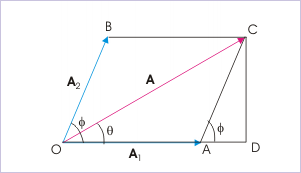
This understanding serves our purpose. If we know amplitudes of individual SHMs and the phase difference, then we can find amplitude of the resulting SHM directly using vector sum formula. It is also evident that vector method can be used to find the resulting phase difference. From the figure,

Notification Switch
Would you like to follow the 'Oscillation and wave motion' conversation and receive update notifications?