1.6 Composition of harmonic motions  (Page 3/3)

$$\tan \theta =\frac{\mathrm{CD}}{\mathrm{OD}}=\frac{A_2\sin \phi }{A_1+A_2\cos \phi }$$

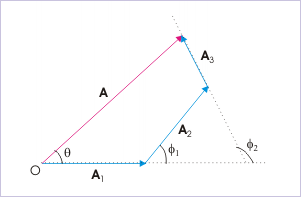
Vector method has one more simplifying aspect. We can compose more than two SHMs by consecutive application of parallelogram theorem or by using consecutive application of triangle law of vector addition. See the figure and observe how do we compose three SHMs and find the resulting amplitude (A) and phase difference (θ) from the reference direction.

Composition of more than two shms

Composition of shms in perpendicular directions

Simple harmonic motions in mutually perpendicular directions constitute a two dimensional motion. The x-direction of motion is governed by SHM force in x-direction, whereas y-direction of motion is governed by SHM force in y-direction. Let the displacements in “x” and “y” directions be :

$$x=A\sin \omega t$$

$$y=B\sin \left(\omega t+\phi \right)$$

The force in x-direction does not affect the displacement in y-direction and vice versa. We have pointed out that “effect” of one force is independent of the presence of other forces. Here, this independence is a step ahead. Force in one direction is incapable to produce “effect” in perpendicular direction in the first place. As such, the two equations, as they are, give “x” and “y” coordinates of the particle at any given instant. The resulting motion is two dimensional motion. In the nutshell, we do not need to combine effects (displacements) in a particular direction as in the case of one dimensional composition.

Lissajous curves

The plot of the motion as defined by the SHM displacement equations is known as “Lissajous curve”. In order to determine the curve (path) of resulting motion, we eliminate “t” from two equations. For this, we first expand the trigonometric expression of displacement in “y” direction :

$$y=B\left(\sin \omega t\cos \phi +\cos \omega t\sin \phi \right)$$

Now, we substitute the values of trigonometric functions from the expression of displacement in “x” direction. Here,

$$\sin \omega t=\frac{x}{A}\text{and}\cos \omega t=\sqrt{\left(1-\frac{x^2}{A^2}\right)}$$

Substituting these values,

$$\Rightarrow y=B\{\frac{x}{A}\cos \phi +\sqrt{\left(1-\frac{x^2}{A^2}\right)}\sin \phi \}$$

$$\Rightarrow \frac{y}{B}-\frac{x}{A}\cos \phi =\sqrt{\left(1-\frac{x^2}{A^2}\right)}\sin \phi$$

Squaring both sides and rearranging,

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy\cos \phi }{AB}={\sin }^2\phi$$

This is an equation of ellipse. The nature of path depends on amplitudes of the individual SHMs and the phase difference. Importantly, we realize that resulting motion may not be oscillatory at all – although it is periodic.

Lissajous curves

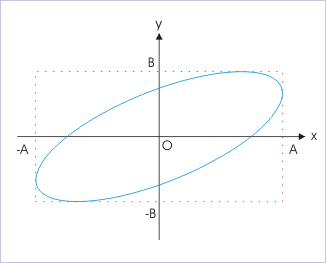
Further, we observe from the equation for displacement in “x” direction that values of “x” lie between “-A” and “A”. Similarly, values of “y” lie between “-B” and “B”. Clearly, path of resulting motion (i.e. ellipse) lies within the boundary, set up by limiting values of “x” and “y”. This is shown in the figure above.

Important cases

We ,here, consider few interesting cases :

Phase difference is zero

Zero phase difference means that individual SHMs are in phase with respect to each other. If we compare two SHMs as if they are independent and separate, then they reach mean position and respective “x” and “y” extremes at the same time. We can find the path of resulting motion by putting phase difference zero in the equation of path. Here,

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy\cos 0^0}{AB}={\sin }^2{0}^0$$

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy}{AB}=0$$

$$\Rightarrow {\left(\frac{x}{A}-\frac{y}{B}\right)}^2=0$$

$$\Rightarrow y=\frac{B}{A}x$$

Lissajous curves

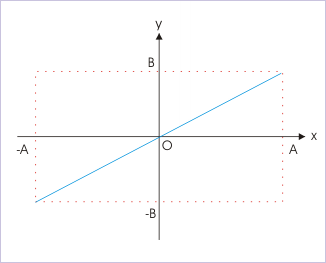
This is the equation of a straight line. The path of motion in reference to bounding rectangle is shown for this case. It is worth pointing here that we can actually derive this equation directly simply by putting φ = 0 in displacement equations in “x” and “y” directions and then solving for "y".

Clearly, motion of the particle under this condition is an oscillatory motion along a straight line. We need to know the resultant displacement equation. Let “z” denotes displacement along the path. By geometry, we have :

$$z=\sqrt{\left(x^2+y^2\right)}$$

Substituting for “x” and “y” with φ = 0,

$$z=\sqrt{\left(A^2{\sin }^2\omega t+B^2{\sin }^2\omega t\right)}=\sqrt{\left(A^2+B^2\right)}\sin \omega t$$

This is bounded periodic harmonic sine function representing SHM of amplitude $\sqrt{\left(A^2+B^2\right)}$ and angular frequency “ω” – same as that of either of the component SHMs.

Phase difference is π/2

A finite phase difference means that individual SHMs are not in phase with respect to each other. If we compare two SHMs as if they are independent and separate, then they reach mean position and respective “x” and “y” extremes at different times. When one is at the mean position, other SHM is at the extreme position and vice versa. We can find the path of resulting motion by putting phase difference “π/2” in the equation of path. Here,

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy\cos \frac{\pi }{2}}{AB}={\sin }^2\frac{\pi }{2}$$

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}=1$$

Lissajous curves

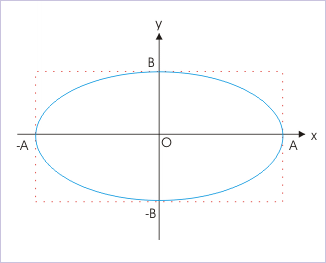
This is an equation of ellipse having major and minor axes “2A” and “2B” respectively. The resulting motion of the particle is along an ellipse. Hence, motion is periodic, but not oscillatory. If A = B, then the equation of path reduces to that of a circle of radius “A” or “B” :

Lissajous curves

$$x^2+y^2=A^2$$

Phase difference is π

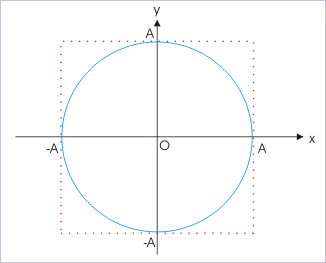
Individual SHMs are not in phase with respect to each other. When one is at one extreme, other SHM is at the other extreme position and vice versa. We can find the path of resulting motion by putting phase difference “π” in the equation of path. Here,

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy\cos \pi }{AB}=\sin {}^2\pi$$

$$\Rightarrow \frac{x^2}{A^2}+\frac{y^2}{B^2}+\frac{2xy}{AB}=0$$

$$\Rightarrow {\left(\frac{x}{A}+\frac{y}{B}\right)}^2=0$$

$$\Rightarrow y=-\frac{B}{A}x$$

Lissajous curves

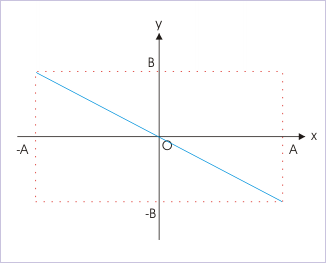
This is the equation of a straight line. The path of motion in reference to bounding rectangle is shown for this case. It is worth pointing here that we can actually derive this equation directly by putting "φ = π" in displacement equations in “x” and “y” directions.

Clearly, motion of the particle under this condition is an oscillatory motion along a straight line. We need to know the resultant displacement equation. Let “z” denotes displacement along the path. By geometry, we have :

$$z=\sqrt{\left(x^2+y^2\right)}$$

$$x=A\sin \omega t$$

$$y=B\sin \left(\omega t+\phi \right)=B\sin \left(\omega t+\phi \right)=-B\sin \omega t$$

Substituting for “x” and “y” with φ = π,

$$\Rightarrow z=\sqrt{\{{\left(A\sin \omega t\right)}^2+{\left(-B\sin \omega t\right)}^2\}}$$

$$\Rightarrow z=\sqrt{\left(A^2{\sin }^2\omega t+B^2{\sin }^2\omega t\right)}=\sqrt{\left(A^2+B^2\right)}\sin \omega t$$

This is bounded periodic harmonic sine function representing SHM of amplitude $\sqrt{\left(A^2+B^2\right)}$ and angular frequency “ω” – same as that of either of the component SHMs.