| << Chapter < Page | Chapter >> Page > |
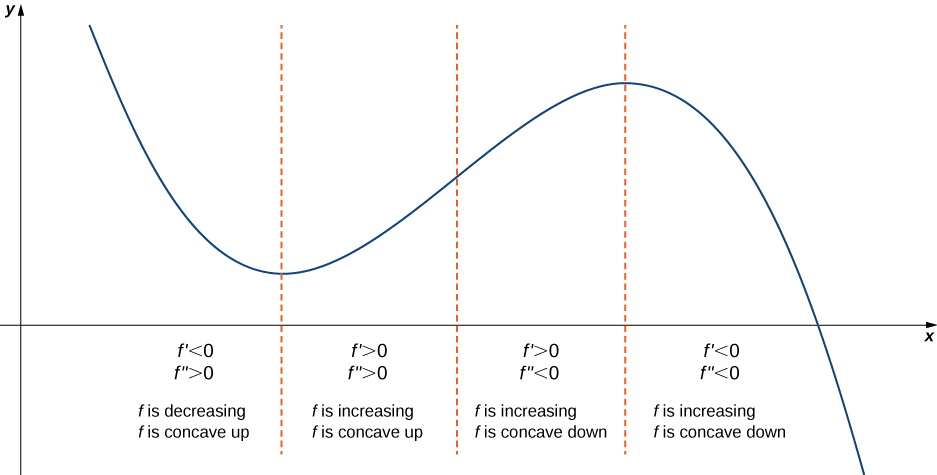
The first derivative test provides an analytical tool for finding local extrema, but the second derivative can also be used to locate extreme values. Using the second derivative can sometimes be a simpler method than using the first derivative.
We know that if a continuous function has a local extrema, it must occur at a critical point. However, a function need not have a local extrema at a critical point. Here we examine how the second derivative test can be used to determine whether a function has a local extremum at a critical point. Let be a twice-differentiable function such that and is continuous over an open interval containing Suppose Since is continuous over for all ( [link] ). Then, by Corollary is a decreasing function over Since we conclude that for all if and if Therefore, by the first derivative test, has a local maximum at On the other hand, suppose there exists a point such that but Since is continuous over an open interval containing then for all ( [link] ). Then, by Corollary is an increasing function over Since we conclude that for all if and if Therefore, by the first derivative test, has a local minimum at
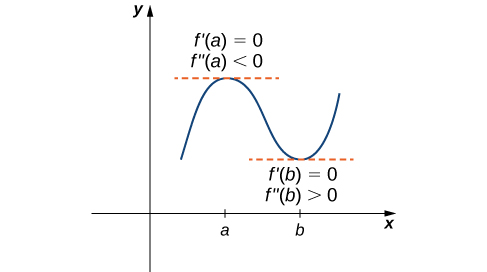
Suppose is continuous over an interval containing
Note that for case iii. when then may have a local maximum, local minimum, or neither at For example, the functions and all have critical points at In each case, the second derivative is zero at However, the function has a local minimum at whereas the function has a local maximum at and the function does not have a local extremum at
Let’s now look at how to use the second derivative test to determine whether has a local maximum or local minimum at a critical point where
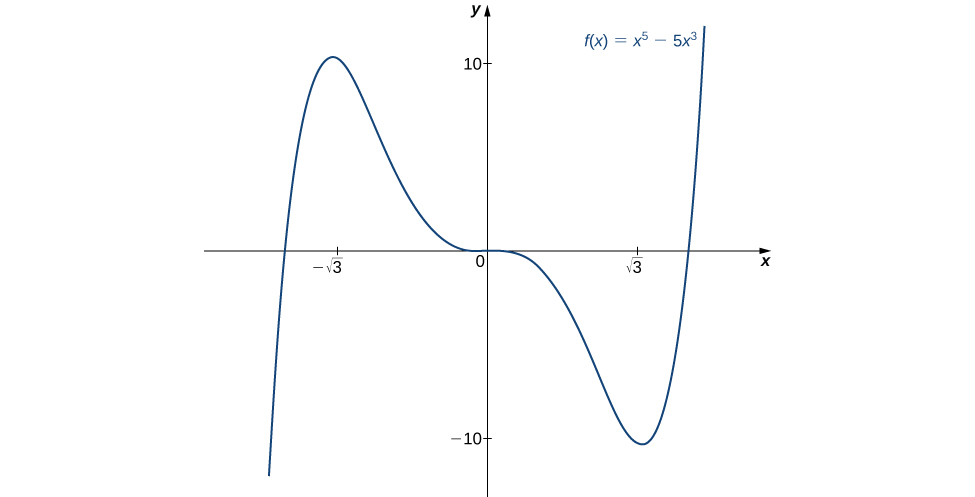
Use the second derivative to find the location of all local extrema for
To apply the second derivative test, we first need to find critical points where The derivative is Therefore, when
To determine whether has a local extrema at any of these points, we need to evaluate the sign of at these points. The second derivative is
In the following table, we evaluate the second derivative at each of the critical points and use the second derivative test to determine whether has a local maximum or local minimum at any of these points.
| Conclusion | ||
|---|---|---|
| Local maximum | ||
| Second derivative test is inconclusive | ||
| Local minimum |
By the second derivative test, we conclude that has a local maximum at and has a local minimum at The second derivative test is inconclusive at To determine whether has a local extrema at we apply the first derivative test. To evaluate the sign of for and let and be the two test points. Since and we conclude that is decreasing on both intervals and, therefore, does not have a local extrema at as shown in the following graph.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?