| << Chapter < Page | Chapter >> Page > |
Verify that the function defined over the interval satisfies the conditions of Rolle’s theorem. Find all points guaranteed by Rolle’s theorem.
Rolle’s theorem is a special case of the Mean Value Theorem. In Rolle’s theorem, we consider differentiable functions that are zero at the endpoints. The Mean Value Theorem generalizes Rolle’s theorem by considering functions that are not necessarily zero at the endpoints. Consequently, we can view the Mean Value Theorem as a slanted version of Rolle’s theorem ( [link] ). The Mean Value Theorem states that if is continuous over the closed interval and differentiable over the open interval then there exists a point such that the tangent line to the graph of at is parallel to the secant line connecting and
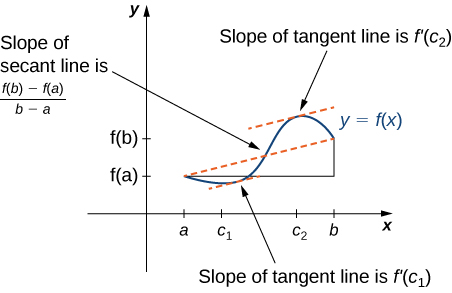
Let be continuous over the closed interval and differentiable over the open interval Then, there exists at least one point such that
The proof follows from Rolle’s theorem by introducing an appropriate function that satisfies the criteria of Rolle’s theorem. Consider the line connecting and Since the slope of that line is
and the line passes through the point the equation of that line can be written as
Let denote the vertical difference between the point and the point on that line. Therefore,
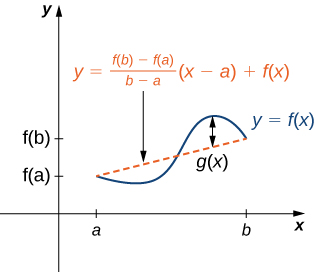
Since the graph of intersects the secant line when and we see that Since is a differentiable function over is also a differentiable function over Furthermore, since is continuous over is also continuous over Therefore, satisfies the criteria of Rolle’s theorem. Consequently, there exists a point such that Since
we see that
Since we conclude that
□
In the next example, we show how the Mean Value Theorem can be applied to the function over the interval The method is the same for other functions, although sometimes with more interesting consequences.
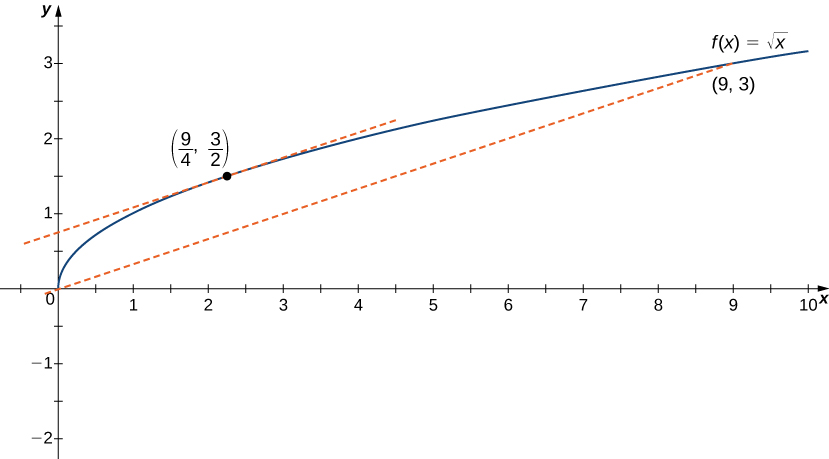
For over the interval show that satisfies the hypothesis of the Mean Value Theorem, and therefore there exists at least one value such that is equal to the slope of the line connecting and Find these values guaranteed by the Mean Value Theorem.
We know that is continuous over and differentiable over Therefore, satisfies the hypotheses of the Mean Value Theorem, and there must exist at least one value such that is equal to the slope of the line connecting and ( [link] ). To determine which value(s) of are guaranteed, first calculate the derivative of The derivative The slope of the line connecting and is given by
We want to find such that That is, we want to find such that
Solving this equation for we obtain At this point, the slope of the tangent line equals the slope of the line joining the endpoints.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?