| << Chapter < Page | Chapter >> Page > |
Since is a differentiable function, by the Mean Value Theorem, there exists such that
Therefore, there exists such that which contradicts the assumption that for all
□
From [link] , it follows that if two functions have the same derivative, they differ by, at most, a constant.
If and are differentiable over an interval and for all then for some constant
Let Then, for all By Corollary 1, there is a constant such that for all Therefore, for all
□
The third corollary of the Mean Value Theorem discusses when a function is increasing and when it is decreasing. Recall that a function is increasing over if whenever whereas is decreasing over if whenever Using the Mean Value Theorem, we can show that if the derivative of a function is positive, then the function is increasing; if the derivative is negative, then the function is decreasing ( [link] ). We make use of this fact in the next section, where we show how to use the derivative of a function to locate local maximum and minimum values of the function, and how to determine the shape of the graph.
This fact is important because it means that for a given function if there exists a function such that then, the only other functions that have a derivative equal to are for some constant We discuss this result in more detail later in the chapter.
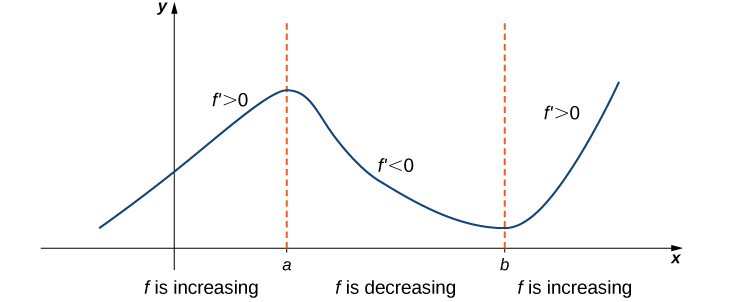
Let be continuous over the closed interval and differentiable over the open interval
We will prove i.; the proof of ii. is similar. Suppose is not an increasing function on Then there exist and in such that but Since is a differentiable function over by the Mean Value Theorem there exists such that
Since we know that Also, tells us that We conclude that
However, for all This is a contradiction, and therefore must be an increasing function over
□

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?