| << Chapter < Page | Chapter >> Page > |
When velocity is a constant, the area under the curve is just velocity times time. This idea is already very familiar. If a car travels away from its starting position in a straight line at a speed of 75 mph for 2 hours, then it is 150 mi away from its original position ( [link] ). Using integral notation, we have
![A graph in quadrant 1 with the x-axis labeled as t (hours) and y-axis labeled as v (mi/hr). The area under the line v(t) = 75 is shaded blue over [0,2].](/ocw/mirror/col11964/m53631/CNX_Calc_Figure_05_02_015.jpg)
In the context of displacement, net signed area allows us to take direction into account. If a car travels straight north at a speed of 60 mph for 2 hours, it is 120 mi north of its starting position. If the car then turns around and travels south at a speed of 40 mph for 3 hours, it will be back at it starting position ( [link] ). Again, using integral notation, we have
In this case the displacement is zero.
![A graph in quadrants one and four with the x-axis labeled as t (hours) and the y axis labeled as v (mi/hr). The first part of the graph is the line v(t) = 60 over [0,2], and the area under the line in quadrant one is shaded. The second part of the graph is the line v(t) = -40 over [2,5], and the area above the line in quadrant four is shaded.](/ocw/mirror/col11964/m53631/CNX_Calc_Figure_05_02_016.jpg)
Suppose we want to know how far the car travels overall, regardless of direction. In this case, we want to know the area between the curve and the x -axis, regardless of whether that area is above or below the axis. This is called the total area .
Graphically, it is easiest to think of calculating total area by adding the areas above the axis and the areas below the axis (rather than subtracting the areas below the axis, as we did with net signed area). To accomplish this mathematically, we use the absolute value function. Thus, the total distance traveled by the car is
Bringing these ideas together formally, we state the following definitions.
Let be an integrable function defined on an interval Let A 1 represent the area between and the x -axis that lies above the axis and let A 2 represent the area between and the x -axis that lies below the axis. Then, the net signed area between and the x -axis is given by
The total area between and the x -axis is given by
Find the total area between and the x -axis over the interval
Calculate the x -intercept as (set solve for x ). To find the total area, take the area below the x -axis over the subinterval and add it to the area above the x -axis on the subinterval ( [link] ).
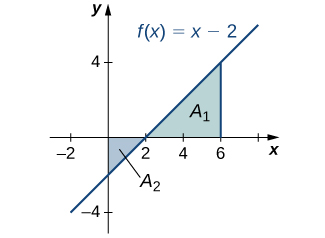
We have
Then, using the formula for the area of a triangle, we obtain
The total area, then, is
Find the total area between the function and the x -axis over the interval
18
The properties of indefinite integrals apply to definite integrals as well. Definite integrals also have properties that relate to the limits of integration. These properties, along with the rules of integration that we examine later in this chapter, help us manipulate expressions to evaluate definite integrals.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?