| << Chapter < Page | Chapter >> Page > |
Use the formula for the area of a trapezoid to evaluate
18 square units
When we defined the definite integral, we lifted the requirement that be nonnegative. But how do we interpret “the area under the curve” when is negative?
Let us return to the Riemann sum. Consider, for example, the function (shown in [link] ) on the interval Use and choose as the left endpoint of each interval. Construct a rectangle on each subinterval of height and width Δ x . When is positive, the product represents the area of the rectangle, as before. When is negative, however, the product represents the negative of the area of the rectangle. The Riemann sum then becomes
![A graph of a downward opening parabola over [-1, 2] with vertex at (0,2) and x-intercepts at (-1,0) and (1,0). Eight rectangles are drawn evenly over [0,2] with heights determined by the value of the function at the left endpoints of each.](/ocw/mirror/col11964/m53631/CNX_Calc_Figure_05_02_003.jpg)
Taking the limit as the Riemann sum approaches the area between the curve above the x -axis and the x -axis, less the area between the curve below the x -axis and the x -axis, as shown in [link] . Then,
The quantity is called the net signed area .
![A graph of a downward opening parabola over [-2, 2] with vertex at (0,2) and x-intercepts at (-1,0) and (1,0). The area in quadrant one under the curve is shaded blue and labeled A1. The area in quadrant four above the curve and to the left of x=2 is shaded blue and labeled A2.](/ocw/mirror/col11964/m53631/CNX_Calc_Figure_05_02_002.jpg)
Notice that net signed area can be positive, negative, or zero. If the area above the x -axis is larger, the net signed area is positive. If the area below the x -axis is larger, the net signed area is negative. If the areas above and below the x -axis are equal, the net signed area is zero.
Find the net signed area between the curve of the function and the x -axis over the interval
The function produces a straight line that forms two triangles: one from to and the other from to ( [link] ). Using the geometric formula for the area of a triangle, the area of triangle A 1 , above the axis, is
where 3 is the base and is the height. The area of triangle A 2 , below the axis, is
where 3 is the base and 6 is the height. Thus, the net area is
![A graph of an increasing line over [-6, 6] going through the origin and (-3, -6) and (3,6). The area under the line in quadrant one over [0,3] is shaded blue and labeled A1, and the area above the line in quadrant three over [-3,0] is shaded blue and labeled A2.](/ocw/mirror/col11964/m53631/CNX_Calc_Figure_05_02_005.jpg)
Analysis
If A 1 is the area above the x -axis and A 2 is the area below the x -axis, then the net area is Since the areas of the two triangles are equal, the net area is zero.
Find the net signed area of over the interval illustrated in the following image.
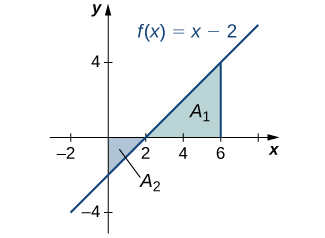
6
One application of the definite integral is finding displacement when given a velocity function. If represents the velocity of an object as a function of time, then the area under the curve tells us how far the object is from its original position. This is a very important application of the definite integral, and we examine it in more detail later in the chapter. For now, we’re just going to look at some basics to get a feel for how this works by studying constant velocities.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?