1.2 Basic classes of functions  (Page 3/28)

Polynomials

A linear function is a special type of a more general class of functions: polynomials. A polynomial function    is any function that can be written in the form

for some integer $n\ge 0$ and constants $a_n,a_{n-1}\text{,…,}{a}_0,$ where $a_n\ne 0.$ In the case when $n=0,$ we allow for $a_0=0;$ if $a_0=0,$ the function $f(x)=0$ is called the zero function . The value $n$ is called the degree    of the polynomial; the constant $a_n$ is called the leading coefficient . A linear function of the form $f\left(x\right)=mx+b$ is a polynomial of degree 1 if $m\ne 0$ and degree 0 if $m=0.$ A polynomial of degree 0 is also called a constant function . A polynomial function of degree 2 is called a quadratic function    . In particular, a quadratic function has the form $f\left(x\right)=a{x}^2+bx+c,$ where $a\ne 0.$ A polynomial function of degree $3$ is called a cubic function    .

Power functions

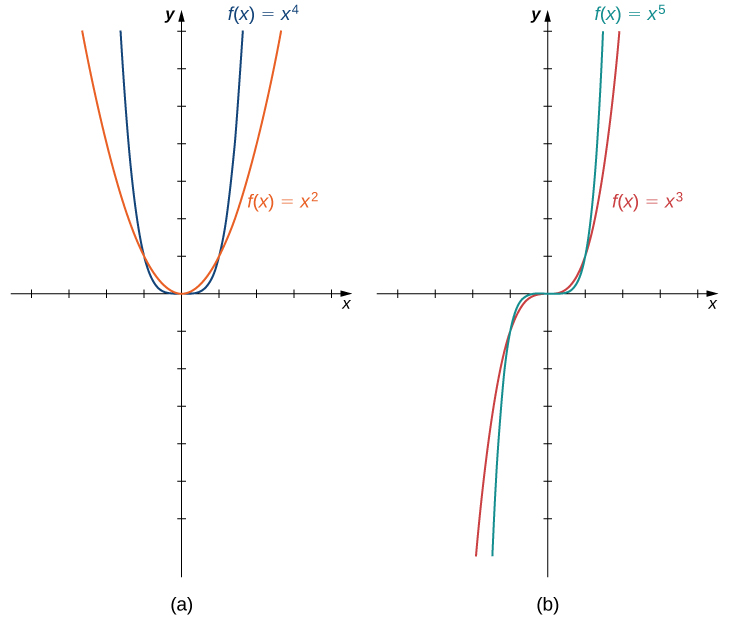
Some polynomial functions are power functions. A power function    is any function of the form $f(x)=a{x}^b,$ where $a$ and $b$ are any real numbers. The exponent in a power function can be any real number, but here we consider the case when the exponent is a positive integer. (We consider other cases later.) If the exponent is a positive integer, then $f(x)=a{x}^n$ is a polynomial. If $n$ is even, then $f(x)=a{x}^n$ is an even function because $f(\text{−}\mathit{\text{x}})=a{(\text{−}\mathit{\text{x}})}^n=a{x}^n$ if $n$ is even. If $n$ is odd, then $f(x)=a{x}^n$ is an odd function because $f(\text{−}\mathit{\text{x}})=a{(\text{−}\mathit{\text{x}})}^n=\text{−}a{x}^n$ if $n$ is odd ( [link] ).

Behavior at infinity

To determine the behavior of a function $f$ as the inputs approach infinity, we look at the values $f(x)$ as the inputs, $x,$ become larger. For some functions, the values of $f(x)$ approach a finite number. For example, for the function $f\left(x\right)=2+1\text{/}x,$ the values $1\text{/}x$ become closer and closer to zero for all values of $x$ as they get larger and larger. For this function, we say $\text{“}f(x)$ approaches two as $x$ goes to infinity,” and we write $f\left(x\right)\to 2$ as $x\to \infty .$ The line $y=2$ is a horizontal asymptote for the function $f\left(x\right)=2+1\text{/}x$ because the graph of the function gets closer to the line as $x$ gets larger.

For other functions, the values $f(x)$ may not approach a finite number but instead may become larger for all values of $x$ as they get larger. In that case, we say $\text{“}f(x)$ approaches infinity as $x$ approaches infinity,” and we write $f\left(x\right)\to \infty$ as $x\to \infty .$ For example, for the function $f\left(x\right)=3x^2,$ the outputs $f(x)$ become larger as the inputs $x$ get larger. We can conclude that the function $f(x)=3x^2$ approaches infinity as $x$ approaches infinity, and we write $3x^2\to \infty$ as $x\to \infty .$ The behavior as $x\to \text{−}\infty$ and the meaning of $f\left(x\right)\to \text{−}\infty$ as $x\to \infty$ or $x\to \text{−}\infty$ can be defined similarly. We can describe what happens to the values of $f(x)$ as $x\to \infty$ and as $x\to \text{−}\infty$ as the end behavior of the function.

To understand the end behavior for polynomial functions, we can focus on quadratic and cubic functions. The behavior for higher-degree polynomials can be analyzed similarly. Consider a quadratic function $f\left(x\right)=a{x}^2+bx+c.$ If $a>0,$ the values $f\left(x\right)\to \infty$ as $x\to \text{±}\infty .$ If $a<0,$ the values $f\left(x\right)\to \text{−∞}$ as $x\to \text{±}\infty .$ Since the graph of a quadratic function is a parabola, the parabola opens upward if $a>0;$ the parabola opens downward if $a<0.$ (See [link] (a).)