1. Home
  2. Calculus volume 1
  3. Functions and graphs
  4. Basic classes of functions

1.2 Basic classes of functions  (Page 5/28)

<< Chapter < Page
  Calculus volume 1     Page 5 / 28
Chapter >> Page >

Consider the quadratic function f ( x ) = 3 x 2 − 6 x + 2 . Find the zeros of f . Does the parabola open upward or downward?

The zeros are x = 1 ± 3 / 3 . The parabola opens upward.

Got questions? Get instant answers now!

Mathematical models

A large variety of real-world situations can be described using mathematical models . A mathematical model is a method of simulating real-life situations with mathematical equations. Physicists, engineers, economists, and other researchers develop models by combining observation with quantitative data to develop equations, functions, graphs, and other mathematical tools to describe the behavior of various systems accurately. Models are useful because they help predict future outcomes. Examples of mathematical models include the study of population dynamics, investigations of weather patterns, and predictions of product sales.

As an example, let’s consider a mathematical model that a company could use to describe its revenue for the sale of a particular item. The amount of revenue R a company receives for the sale of n items sold at a price of p dollars per item is described by the equation R = p · n . The company is interested in how the sales change as the price of the item changes. Suppose the data in [link] show the number of units a company sells as a function of the price per item.

Number of units sold n (in thousands) as a function of price per unit p (in dollars)
p 6 8 10 12 14
n 19.4 18.5 16.2 13.8 12.2

In [link] , we see the graph the number of units sold (in thousands) as a function of price (in dollars). We note from the shape of the graph that the number of units sold is likely a linear function of price per item, and the data can be closely approximated by the linear function n = −1.04 p + 26 for 0 ≤ p ≤ 25 , where n predicts the number of units sold in thousands. Using this linear function, the revenue (in thousands of dollars) can be estimated by the quadratic function

R ( p ) = p · ( −1.04 p + 26 ) = −1.04 p 2 + 26 p

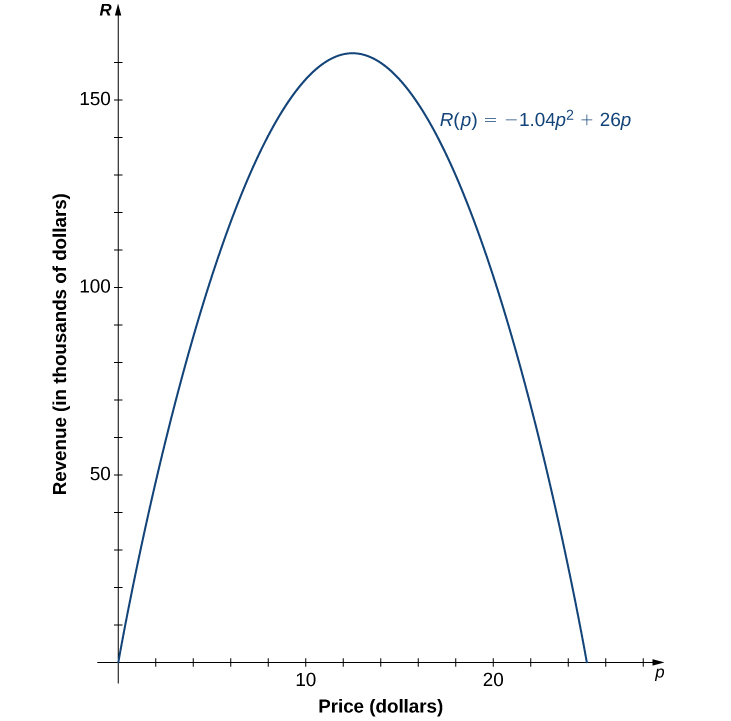
for 0 ≤ p ≤ 25 . In [link] , we use this quadratic function to predict the amount of revenue the company receives depending on the price the company charges per item. Note that we cannot conclude definitively the actual number of units sold for values of p , for which no data are collected. However, given the other data values and the graph shown, it seems reasonable that the number of units sold (in thousands) if the price charged is p dollars may be close to the values predicted by the linear function n = −1.04 p + 26 .

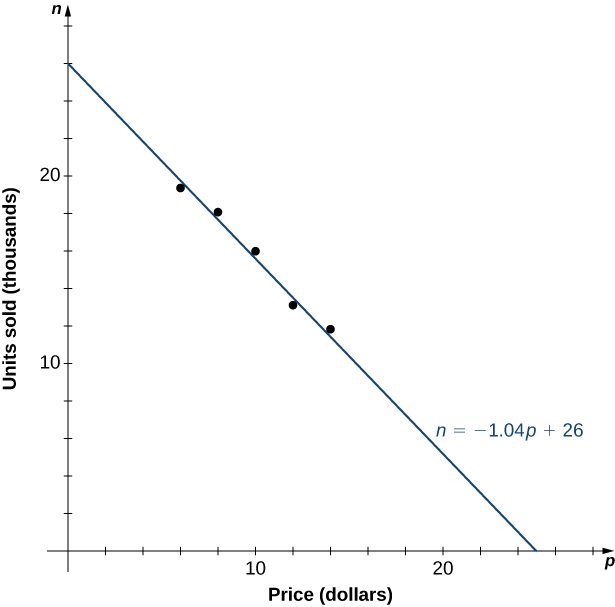
An image of a graph. The y axis runs from 0 to 28 and is labeled “n, units sold in thousands”. The x axis runs from 0 to 28 and is labeled “p, price in dollars”. The graph is of the function “n = -1.04p + 26”, which is a decreasing line function that starts at the y intercept point (0, 26). There are 5 points plotted on the graph at (6, 19.4), (8, 18.5), (10, 16.2), (12, 13.8), and (14, 12.2). The points are not on the graph of the function line, but are very close to it. The function has an x intercept at the point (25, 0).
The data collected for the number of items sold as a function of price is roughly linear. We use the linear function n = −1.04 p + 26 to estimate this function.

Maximizing revenue

A company is interested in predicting the amount of revenue it will receive depending on the price it charges for a particular item. Using the data from [link] , the company arrives at the following quadratic function to model revenue R as a function of price per item p :

R ( p ) = p · ( −1.04 p + 26 ) = −1.04 p 2 + 26 p

for 0 ≤ p ≤ 25 .

  1. Predict the revenue if the company sells the item at a price of p = $ 5 and p = $ 17 .
  2. Find the zeros of this function and interpret the meaning of the zeros.
  3. Sketch a graph of R .
  4. Use the graph to determine the value of p that maximizes revenue. Find the maximum revenue.
  1. Evaluating the revenue function at p = 5 and p = 17 , we can conclude that
    R ( 5 ) = −1.04 ( 5 ) 2 + 26 ( 5 ) = 104 , so revenue = $104,000; R ( 17 ) = −1.04 ( 17 ) 2 + 26 ( 17 ) = 141.44 , so revenue = $144,440.
  2. The zeros of this function can be found by solving the equation −1.04 p 2 + 26 p = 0 . When we factor the quadratic expression, we get p ( −1.04 p + 26 ) = 0 . The solutions to this equation are given by p = 0 , 25 . For these values of p , the revenue is zero. When p = $ 0 , the revenue is zero because the company is giving away its merchandise for free. When p = $ 25 , the revenue is zero because the price is too high, and no one will buy any items.
  3. Knowing the fact that the function is quadratic, we also know the graph is a parabola. Since the leading coefficient is negative, the parabola opens downward. One property of parabolas is that they are symmetric about the axis, so since the zeros are at p = 0 and p = 25 , the parabola must be symmetric about the line halfway between them, or p = 12.5 .
    An image of a graph. The y axis runs from 0 to 170 and is labeled “R, revenue in thousands of dollars”. The x axis runs from 0 to 28 and is labeled “p, price in dollars”. The graph is of the function “n = -1.04(p squared) + 26p”, which is a parabola that starts at the origin. The function increases until the maximum point at (12.5, 162.5) and then begins decreasing. The function has x intercepts at the origin and the point (25, 0). The y intercept is at the origin.
  4. The function is a parabola with zeros at p = 0 and p = 25 , and it is symmetric about the line p = 12.5 , so the maximum revenue occurs at a price of p = $ 12.50 per item. At that price, the revenue is R ( p ) = −1.04 ( 12.5 ) 2 + 26 ( 12.5 ) = $ 162 , 500 .
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 17

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 1. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11964/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?

Ask