2.5 The precise definition of a limit  (Page 19/8)

By now you have progressed from the very informal definition of a limit in the introduction of this chapter to the intuitive understanding of a limit. At this point, you should have a very strong intuitive sense of what the limit of a function means and how you can find it. In this section, we convert this intuitive idea of a limit into a formal definition using precise mathematical language. The formal definition of a limit is quite possibly one of the most challenging definitions you will encounter early in your study of calculus; however, it is well worth any effort you make to reconcile it with your intuitive notion of a limit. Understanding this definition is the key that opens the door to a better understanding of calculus.

Quantifying closeness

Before stating the formal definition of a limit, we must introduce a few preliminary ideas. Recall that the distance between two points a and b on a number line is given by $\left|a-b\right|.$

• The statement $\left|f\left(x\right)-L\right|<\epsilon$ may be interpreted as: The distance between $f\left(x\right)$ and L is less than ε.
• The statement $0<\left|x-a\right|<\delta$ may be interpreted as: $x\ne a$ and the distance between x and a is less than δ.

It is also important to look at the following equivalences for absolute value:

• The statement $\left|f\left(x\right)-L\right|<\epsilon$ is equivalent to the statement $L-\epsilon <f\left(x\right)<L+\epsilon .$
• The statement $0<\left|x-a\right|<\delta$ is equivalent to the statement $a-\delta <x<a+\delta$ and $x\ne a.$

With these clarifications, we can state the formal epsilon-delta definition of the limit    .

This definition may seem rather complex from a mathematical point of view, but it becomes easier to understand if we break it down phrase by phrase. The statement itself involves something called a universal quantifier (for every $\epsilon >0\text{),}$ an existential quantifier (there exists a $\delta >0\text{),}$ and, last, a conditional statement (if $0<\left|x-a\right|<\delta ,$ then $\left|f\left(x\right)-L\right|<\epsilon \text{).}$ Let’s take a look at [link] , which breaks down the definition and translates each part.

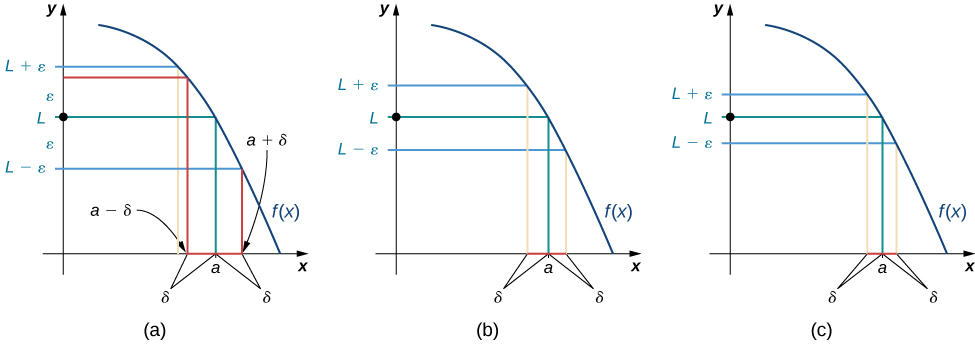
We can get a better handle on this definition by looking at the definition geometrically. [link] shows possible values of $\delta$ for various choices of $\epsilon >0$ for a given function $f\left(x\right),$ a number a , and a limit L at a . Notice that as we choose smaller values of ε (the distance between the function and the limit), we can always find a $\delta$ small enough so that if we have chosen an x value within $\delta$ of a , then the value of $f\left(x\right)$ is within ε of the limit L .