| << Chapter < Page | Chapter >> Page > |
Mark is attempting to build muscle mass and so he needs to eat at least an additional 80 grams of protein a day. A bottle of protein water costs $3.20 and a protein bar costs $1.75. The protein water supplies 27 grams of protein and the bar supplies 16 gram. If he has $ 10 dollars to spend
ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Could he buy 3 bottles of protein water and 1 protein bar?
ⓓ Could he buy no bottles of protein water and 5 protein bars?
Jocelyn desires to increase both her protein consumption and caloric intake. She desires to have at least 35 more grams of protein each day and no more than an additional 200 calories daily. An ounce of cheddar cheese has 7 grams of protein and 110 calories. An ounce of parmesan cheese has 11 grams of protein and 22 calories.
ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Could she eat 1 ounce of cheddar cheese and 3 ounces of parmesan cheese?
ⓓ Could she eat 2 ounces of cheddar cheese and 1 ounce of parmesan cheese?
Mark is increasing his exercise routine by running and walking at least 4 miles each day. His goal is to burn a minimum of 1,500 calories from this exercise. Walking burns 270 calories/mile and running burns 650 calories.
ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Could he meet his goal by walking 3 miles and running 1 mile?
ⓓ Could he meet his goal by walking 2 miles and running 2 mile?
Tickets for an American Baseball League game for 3 adults and 3 children cost less than $75, while tickets for 2 adults and 4 children cost less than $62.
ⓐ Write a system of inequalities to model this problem.
ⓑ Graph the system.
ⓒ Could the tickets cost $20 for adults and $8 for children?
ⓓ Could the tickets cost $15 for adults and $5 for children?
Grandpa and Grandma are treating their family to the movies. Matinee tickets cost $4 per child and $4 per adult. Evening tickets cost $6 per child and $8 per adult. They plan on spending no more than $80 on the matinee tickets and no more than $100 on the evening tickets.
ⓐ Write a system of inequalities to model this situation.
ⓑ Graph the system.
ⓒ Could they take 9 children and 4 adults to both shows?
ⓓ Could they take 8 children and 5 adults to both shows?
Graph the inequality . How do you know which side of the line should be shaded?
Answers will vary.
Graph the system . What does the solution mean?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
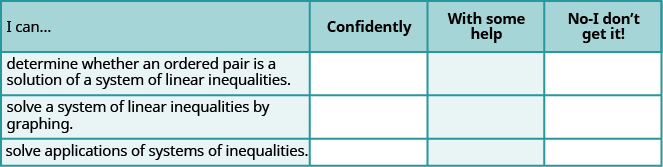
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
Determine Whether an Ordered Pair is a Solution of a System of Equations .
In the following exercises, determine if the following points are solutions to the given system of equations.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?