10.3 Solve quadratic equations using the quadratic formula (Page 3/5)

Elementary algebra Page 3 / 5

When we solved linear equations, if an equation had too many fractions we ‘cleared the fractions’ by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions—to solve. We can use the same strategy with quadratic equations.

Solve $\frac{1}{2} u^{2} + \frac{2}{3} u = \frac{1}{3}$ by using the Quadratic Formula.

Solution


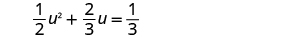Multiply both sides by the LCD, 6, to clear the fractions.
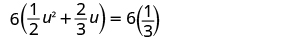Multiply.
Subtract 2 to get the equation in standard form.
Identify the a, b, c values.
Write the Quadratic Formula.
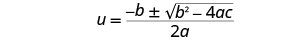Then substitute in the values of a, b, c.
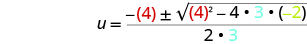Simplify.
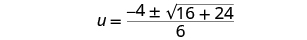
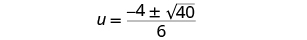Simplify the radical.
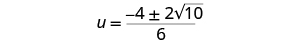Factor out the common factor in the numerator.
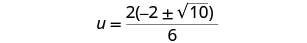Remove the common factors.
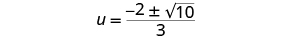Rewrite to show two solutions.
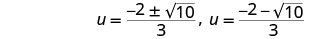Check. We leave the check to you.

Got questions? Get instant answers now!

Solve $\frac{1}{4} c^{2} - \frac{1}{3} c = \frac{1}{12}$ by using the Quadratic Formula.

$c = \frac{2 \pm \sqrt{7}}{3}$

Got questions? Get instant answers now!

Solve $\frac{1}{9} d^{2} - \frac{1}{2} d = - \frac{1}{2}$ by using the Quadratic Formula.

$d = \frac{2}{3}, d = 0$

Got questions? Get instant answers now!

Think about the equation ${(x - 3)}^{2} = 0$ . We know from the Zero Products Principle that this equation has only one solution: $x = 3$ .

We will see in the next example how using the Quadratic Formula to solve an equation with a perfect square also gives just one solution.

Solve $4 x^{2} - 20 x = −25$ by using the Quadratic Formula.

Solution


Add 25 to get the equation in standard form.
Identify the a, b, c values.
Write the Quadratic Formula.
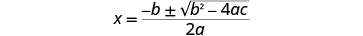Then substitute in the values of a, b, c.
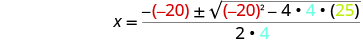Simplify.
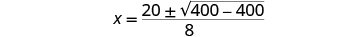
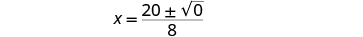Simplify the radical.
Simplify the fraction.
Check. We leave the check to you.

Did you recognize that $4 x^{2} - 20 x + 25$ is a perfect square?

Got questions? Get instant answers now!

Solve $r^{2} + 10 r + 25 = 0$ by using the Quadratic Formula.

$r = −5$

Got questions? Get instant answers now!

Solve $25 t^{2} - 40 t = −16$ by using the Quadratic Formula.

$t = \frac{4}{5}$

Got questions? Get instant answers now!

Use the discriminant to predict the number of solutions of a quadratic equation

When we solved the quadratic equations in the previous examples, sometimes we got two solutions, sometimes one solution, sometimes no real solutions. Is there a way to predict the number of solutions to a quadratic equation without actually solving the equation?

Yes, the quantity inside the radical of the Quadratic Formula makes it easy for us to determine the number of solutions. This quantity is called the discriminant .

Discriminant

In the Quadratic Formula $x = \frac{− b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ , the quantity $b^{2} - 4 a c$ is called the discriminant .

Let’s look at the discriminant of the equations in [link] , [link] , and [link] , and the number of solutions to those quadratic equations.

	Quadratic Equation (in standard form)	Discriminant $b^{2} - 4 a c$	Sign of the Discriminant	Number of real solutions
[link]	$2 x^{2} + 9 x - 5 = 0$	$9^{2} - 4 \cdot 2 (−5) = 121$	+	2
[link]	$4 x^{2} - 20 x + 25 = 0$	${(−20)}^{2} - 4 \cdot 4 \cdot 25 = 0$	0	1
[link]	$3 p^{2} + 2 p + 9 = 0$	$2^{2} - 4 \cdot 3 \cdot 9 = −104$	−	0

When the discriminant is positive $(x = \frac{− b \pm \sqrt{+}}{2 a})$ the quadratic equation has two solutions .

When the discriminant is zero $(x = \frac{− b \pm \sqrt{0}}{2 a})$ the quadratic equation has one solution .

When the discriminant is negative $(x = \frac{− b \pm \sqrt{-}}{2 a})$ the quadratic equation has no real solutions .

Use the discriminant, $b^{2} - 4 a c$ , to determine the number of solutions of a quadratic equation.

For a quadratic equation of the form $a x^{2} + b x + c = 0$ , $a \neq 0$ ,

if $b^{2} - 4 a c > 0$ , the equation has two solutions.
if $b^{2} - 4 a c = 0$ , the equation has one solution.
if $b^{2} - 4 a c < 0$ , the equation has no real solutions.

Determine the number of solutions to each quadratic equation:

Solution

To determine the number of solutions of each quadratic equation, we will look at its discriminant.

ⓐ
$\begin{matrix} 2 v^{2} - 3 v + 6 = 0 \\ The equation is in standard form, identify a, b, c . & a = 2, b = −3, c = 6 \\ Write the discriminant. & b^{2} - 4 a c \\ Substitute in the values of a, b, c . & {(3)}^{2} - 4 \cdot 2 \cdot 6 \\ Simplify. & \begin{matrix} 9 - 48 \\ −39 \end{matrix} \\ Because the discriminant is negative, there are no real \\ solutions to the equation. \end{matrix}$
ⓑ
$\begin{matrix} 3 x^{2} + 7 x - 9 = 0 \\ The equation is in standard form, identify a, b, c . & a = 3, b = 7, c = −9 \\ Write the discriminant. & b^{2} - 4 a c \\ Substitute in the values of a, b, c . & {(7)}^{2} - 4 \cdot 3 \cdot (−9) \\ Simplify. & \begin{matrix} 49 + 108 \\ 157 \end{matrix} \\ Because the discriminant is positive, there are two \\ solutions to the equation. \end{matrix}$
ⓒ
$\begin{matrix} 5 n^{2} + n + 4 = 0 \\ The equation is in standard form, identify a, b, and c . & a = 5, b = 1, c = 4 \\ Write the discriminant. & b^{2} - 4 a c \\ Substitute in the values of a, b, c . & {(1)}^{2} - 4 \cdot 5 \cdot 4 \\ Simplify. & \begin{matrix} 1 - 80 \\ −79 \end{matrix} \\ Because the discriminant is negative, there are no real \\ solutions to the equation. \end{matrix}$
ⓓ
$\begin{matrix} 9 y^{2} - 6 y + 1 = 0 \\ The equation is in standard form, identify a, b, c . & a = 9, b = −6, c = 1 \\ Write the discriminant. & b^{2} - 4 a c \\ Substitute in the values of a, b, c . & {(−6)}^{2} - 4 \cdot 9 \cdot 1 \\ Simplify. & \begin{matrix} 36 - 36 \\ 0 \end{matrix} \\ Because the discriminant is 0, there is one solution to the equation. \end{matrix}$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Elementary algebra' conversation and receive update notifications?

Ask

	9 Physiotherapy Modalities By Rhodes Start Exam
	1 AP Key Terms 01 Human Body Anatomy Physiology By OpenStax Start Key Terms
	Computer System Engineering By Robert Morris Start Exam
	27 Biology 27 Animal Diversity MCQ By OpenStax Start Quiz
	Real Estate Finance Exam 2006 By David Geltner Start Exam
	Tournament Director Quiz By Eddie Unverzagt Start Quiz
	23 AP Key Terms 23 The Digestive System By OpenStax Start Key Terms
	Summer kitchens By Heather McAvoy Start Quiz
	1 Microbiology Final 1 By Madison Christian Start Quiz
	35 Biology 35 The Nervous System MCQ By OpenStax Start Quiz

10.3 Solve quadratic equations using the quadratic formula (Page 3/5)

Solution

Solution

Use the discriminant to predict the number of solutions of a quadratic equation

Discriminant

Use the discriminant, b 2 − 4 a c , to determine the number of solutions of a quadratic equation.

Solution

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Use the discriminant, $b^{2} - 4 a c$ , to determine the number of solutions of a quadratic equation.