| << Chapter < Page | Chapter >> Page > |
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
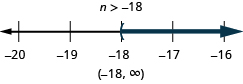
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
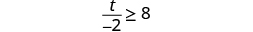 | |
| Multiply both sides of the inequality by
.
Since , the inequality reverses. |
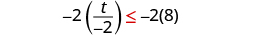 |
| Simplify. |
 |
| Graph the solution on the number line. |
 |
| Write the solution in interval notation. |
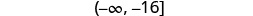 |
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
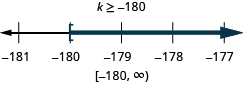
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
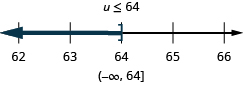
Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but be sure to pay close attention during multiplication or division.
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
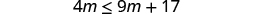 | |
| Subtract from both sides to collect the variables on the left. |
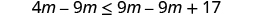 |
| Simplify. |
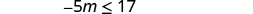 |
| Divide both sides of the inequality by −5, and reverse the inequality. |
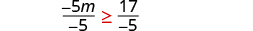 |
| Simplify. |
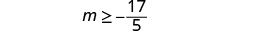 |
| Graph the solution on the number line. |
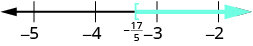 |
| Write the solution in interval notation. |
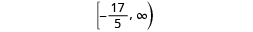 |
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
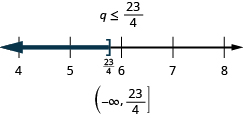
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
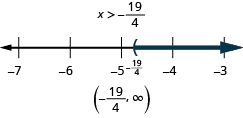
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
| Simplify each side as much as possible. | |
| Distribute. | |
| Combine like terms. | |
| Subtract from both sides to collect the variables on the left. | |
| Simplify. | |
| Add 36 to both sides to collect the constants on the right. | |
| Simplify. | |
| Divide both sides of the inequality by 4; the inequality stays the same. | |
| Simplify. | |
| Graph the solution on the number line. |
 |
| Write the solution in interal notation. |
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
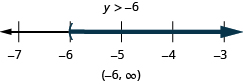
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
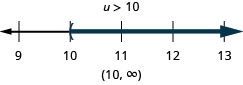
Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.
Solve the inequality , graph the solution on the number line, and write the solution in interval notation.
| Simplify each side as much as possible. | |
| Distribute. | |
| Combine like terms. | |
| Subtract from both sides to collect the variables on the left. | |
| Simplify. | |
| The ’s are gone, and we have a true statement. | The inequality is an identity.
The solution is all real numbers. |
| Graph the solution on the number line. |
 |
| Write the solution in interval notation. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?