| << Chapter < Page | Chapter >> Page > |
Look back at the dividends in [link] , [link] , and [link] . The terms were written in descending order of degrees, and there were no missing degrees. The dividend in [link] will be . It is missing an term. We will add in as a placeholder.
Find the quotient:
Notice that there is no term in the dividend. We will add as a placeholder.
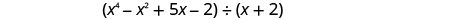 | |
| Write it as a long division problem. Be sure the dividend is in standard form with placeholders for missing terms. |
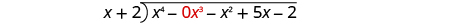 |
| Divide
x
4 by
x .
Put the answer, x 3 , in the quotient over the x 3 term. Multiply x 3 times x + 2. Line up the like terms. Subtract and then bring down the next term. |
 |
| Divide −2
x
3 by
x .
Put the answer, −2 x 2 , in the quotient over the x 2 term. Multiply −2 x 2 times x + 1. Line up the like terms. Subtract and bring down the next term. |
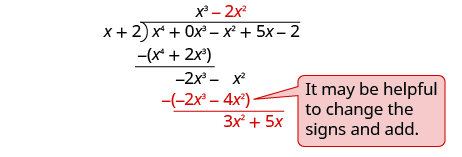 |
| Divide 3
x
2 by
x .
Put the answer, 3 x , in the quotient over the x term. Multiply 3 x times x + 1. Line up the like terms. Subtract and bring down the next term. |
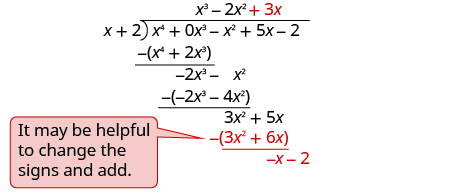 |
| Divide −
x by
x .
Put the answer, −1, in the quotient over the constant term. Multiply −1 times x + 1. Line up the like terms. Change the signs, add. |
 |
| To check, multiply . | |
| The result should be . |
In [link] , we will divide by . As we divide we will have to consider the constants as well as the variables.
Find the quotient:
This time we will show the division all in one step. We need to add two placeholders in order to divide.
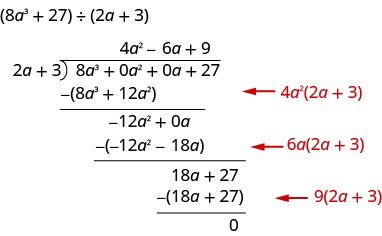
To check, multiply .
The result should be .
Access these online resources for additional instruction and practice with dividing polynomials:
In the following exercises, divide each polynomial by the monomial.
Divide a Polynomial by a Binomial
In the following exercises, divide each polynomial by the binomial.
Average cost Pictures Plus produces digital albums. The company’s average cost (in dollars) to make albums is given by the expression .
Handshakes At a company meeting, every employee shakes hands with every other employee. The number of handshakes is given by the expression , where represents the number of employees. How many handshakes will there be if there are 10 employees at the meeting?
45
James divides by 6 this way: . What is wrong with his reasoning?
Divide and explain with words how you get each term of the quotient.
Answers will vary.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all goals?

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?