6.6 Divide polynomials  (Page 2/3)

Divide a polynomial by a binomial

To divide a polynomial by a binomial    , we follow a procedure very similar to long division of numbers. So let’s look carefully the steps we take when we divide a 3-digit number, 875, by a 2-digit number, 25.

We write the long division
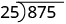We divide the first two digits, 87, by 25.
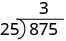We multiply 3 times 25 and write the product under the 87.
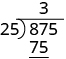Now we subtract 75 from 87.
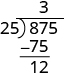Then we bring down the third digit of the dividend, 5.
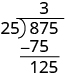Repeat the process, dividing 25 into 125.

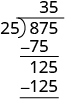We check division by multiplying the quotient by the divisor.

If we did the division correctly, the product should equal the dividend.

Now we will divide a trinomial    by a binomial. As you read through the example, notice how similar the steps are to the numerical example above.

Find the quotient: $\left(x^2+9x+20\right)÷\left(x+5\right).$

Solution

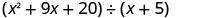Write it as a long division problem.
Be sure the dividend is in standard form.
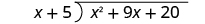Divide x 2 by x . It may help to ask yourself, "What do I need to multiply x by to get x 2 ?"
Put the answer, x , in the quotient over the x term.
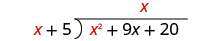Multiply x times x + 5. Line up the like terms under the dividend.
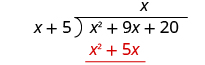Subtract x 2 + 5 x from x 2 + 9 x .
Then bring down the last term, 20.
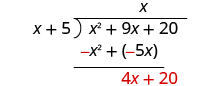Divide 4 x by x . It may help to ask yourself, "What do I need to multiply x by to get 4 x ?"
Put the answer, 4, in the quotient over the constant term.
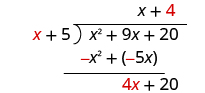Multiply 4 times x + 5.
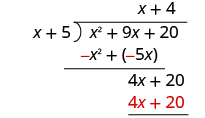Subtract 4 x + 20 from 4 x + 20.
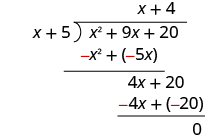Check:
Multiply the quotient by the divisor.
( x + 4)( x + 5)
You should get the dividend.
x 2 + 9 x + 20✓

Got questions? Get instant answers now!

Got questions? Get instant answers now!

When the divisor has subtraction sign, we must be extra careful when we multiply the partial quotient and then subtract. It may be safer to show that we change the signs and then add.

Find the quotient: $\left(2x^2-5x-3\right)÷\left(x-3\right).$

Solution

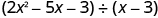Write it as a long division problem.
Be sure the dividend is in standard form.
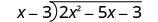Divide 2 x 2 by x . Put the answer, 2 x , in the quotient over the x term.
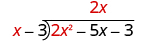Multiply 2 x times x − 3. Line up the like terms under the dividend.
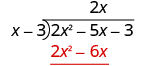Subtract 2 x 2 − 6 x from 2 x 2 − 5 x . Change the signs and then add. Then bring down the last term.
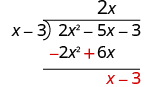Divide x by x . Put the answer, 1, in the quotient over the constant term.
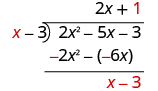Multiply 1 times x − 3.
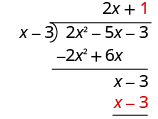Subtract x − 3 from x − 3 by changing the signs and adding.
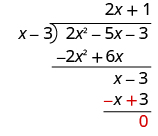To check, multiply ( x − 3)(2 x + 1).
The result should be 2 x 2 − 5 x − 3.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

When we divided 875 by 25, we had no remainder. But sometimes division of numbers does leave a remainder. The same is true when we divide polynomials. In [link] , we’ll have a division that leaves a remainder. We write the remainder as a fraction with the divisor as the denominator.

Find the quotient: $\left(x^3-x^2+x+4\right)÷\left(x+1\right).$

Solution

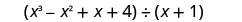Write it as a long division problem.
Be sure the dividend is in standard form.
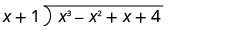Divide x 3 by x . Put the answer, x 2 , in the quotient over the x 2 term. Multiply x 2 times x + 1. Line up the like terms under the dividend.
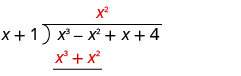Subtract x 3 + x 2 from x 3 − x 2 by changing the signs and adding. Then bring down the next term.
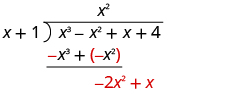Divide −2 x 2 by x . Put the answer, −2 x , in the quotient over the x term. Multiply −2 x times x + 1. Line up the like terms under the dividend.
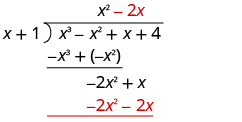Subtract −2 x 2 − 2 x from −2 x 2 + x by changing the signs and adding. Then bring down the last term.
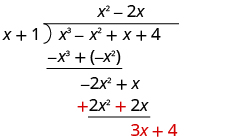Divide 3 x by x . Put the answer, 3, in the quotient over the constant term. Multiply 3 times x + 1. Line up the like terms under the dividend.
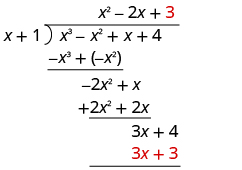Subtract 3 x + 3 from 3 x + 4 by changing the signs and adding. Write the remainder as a fraction with the divisor as the denominator.
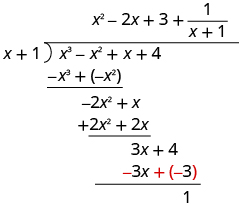To check, multiply $\left(x+1\right)(x^2-2x+3+\frac{1}{x+1}).$ The result should be $x^3-x^2+x+4$ .

Got questions? Get instant answers now!

Got questions? Get instant answers now!