| << Chapter < Page | Chapter >> Page > |
For any algebraic expression and real numbers and where
Solve
Solve
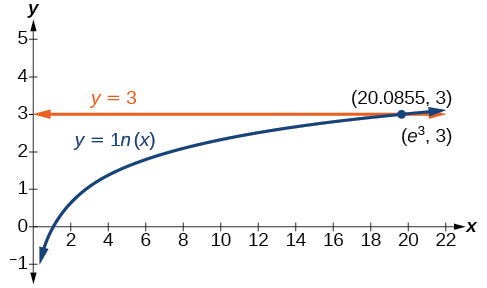
[link] represents the graph of the equation. On the graph, the x -coordinate of the point at which the two graphs intersect is close to 20. In other words A calculator gives a better approximation:
Use a graphing calculator to estimate the approximate solution to the logarithmic equation to 2 decimal places.
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers and any positive real number where
For example,
So, if then we can solve for and we get To check, we can substitute into the original equation: In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
For example, consider the equation To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?