| << Chapter < Page | Chapter >> Page > |
The most common graphs name the input value and the output value and we say is a function of or when the function is named The graph of the function is the set of all points in the plane that satisfies the equation If the function is defined for only a few input values, then the graph of the function consists of only a few points, where the x -coordinate of each point is an input value and the y -coordinate of each point is the corresponding output value. For example, the black dots on the graph in [link] tell us that and However, the set of all points satisfying is a curve. The curve shown includes and because the curve passes through those points.
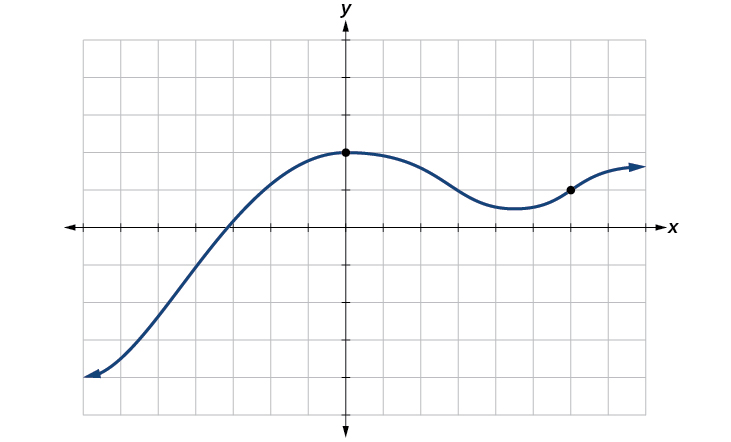
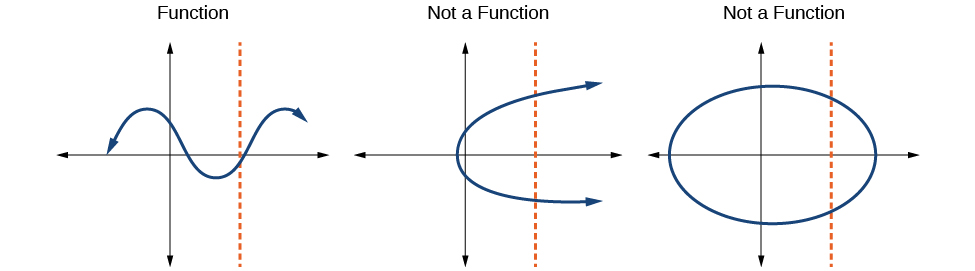
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. See [link] .
Given a graph, use the vertical line test to determine if the graph represents a function.
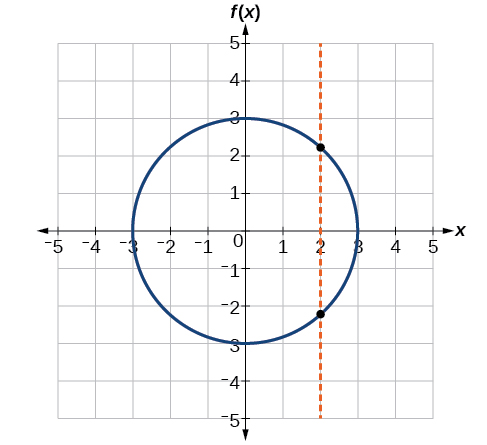
If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in parts (a) and (b) of [link] . From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at most x -values, a vertical line would intersect the graph at more than one point, as shown in [link] .
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test . Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.
Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
Consider the functions shown in [link] (a) and [link] (b) . Are either of the functions one-to-one?
The function in [link] (a) is not one-to-one. The horizontal line shown in [link] intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)

The function in [link] (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once.
Is the graph shown in [link] one-to-one?
No, because it does not pass the horizontal line test.
In this text, we will be exploring functions—the shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start with the alphabet. When learning to do arithmetic, we start with numbers. When working with functions, it is similarly helpful to have a base set of building-block elements. We call these our “toolkit functions,” which form a set of basic named functions for which we know the graph, formula, and special properties. Some of these functions are programmed to individual buttons on many calculators. For these definitions we will use as the input variable and as the output variable.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?