| << Chapter < Page | Chapter >> Page > |
Evaluate
Now, we can evaluate the inverse function as we did earlier.
To evaluate compositions of the form where and are any two of the functions sine, cosine, or tangent and is any input in the domain of we have exact formulas, such as When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
Find an exact value for
Beginning with the inside, we can say there is some angle such that which means and we are looking for We can use the Pythagorean identity to do this.
Since is in quadrant I, must be positive, so the solution is See [link] .
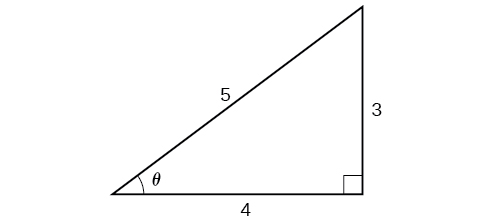
We know that the inverse cosine always gives an angle on the interval so we know that the sine of that angle must be positive; therefore
Find an exact value for
While we could use a similar technique as in [link] , we will demonstrate a different technique here. From the inside, we know there is an angle such that We can envision this as the opposite and adjacent sides on a right triangle, as shown in [link] .
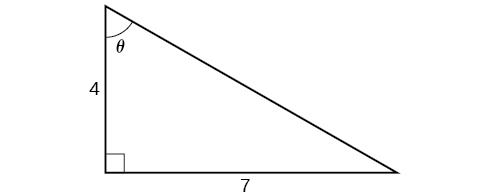
Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.
Now, we can evaluate the sine of the angle as the opposite side divided by the hypotenuse.
This gives us our desired composition.
Find a simplified expression for for
We know there is an angle such that
Because we know that the inverse sine must give an angle on the interval we can deduce that the cosine of that angle must be positive.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?