| << Chapter < Page | Chapter >> Page > |
Because radian measure is the ratio of two lengths, it is a unitless measure. For example, in [link] , suppose the radius were 2 inches and the distance along the arc were also 2 inches. When we calculate the radian measure of the angle, the “inches” cancel, and we have a result without units. Therefore, it is not necessary to write the label “radians” after a radian measure, and if we see an angle that is not labeled with “degrees” or the degree symbol, we can assume that it is a radian measure.
Considering the most basic case, the unit circle (a circle with radius 1), we know that 1 rotation equals 360 degrees, We can also track one rotation around a circle by finding the circumference, and for the unit circle These two different ways to rotate around a circle give us a way to convert from degrees to radians.
In addition to knowing the measurements in degrees and radians of a quarter revolution, a half revolution, and a full revolution, there are other frequently encountered angles in one revolution of a circle with which we should be familiar. It is common to encounter multiples of 30, 45, 60, and 90 degrees. These values are shown in [link] . Memorizing these angles will be very useful as we study the properties associated with angles.
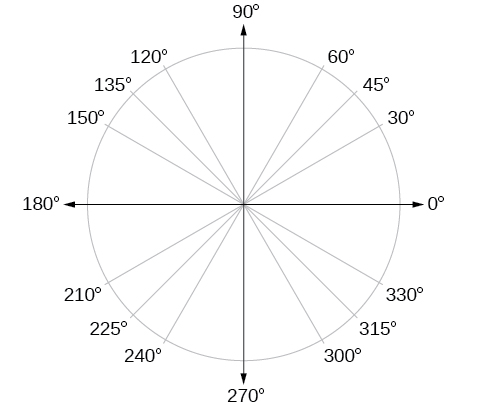
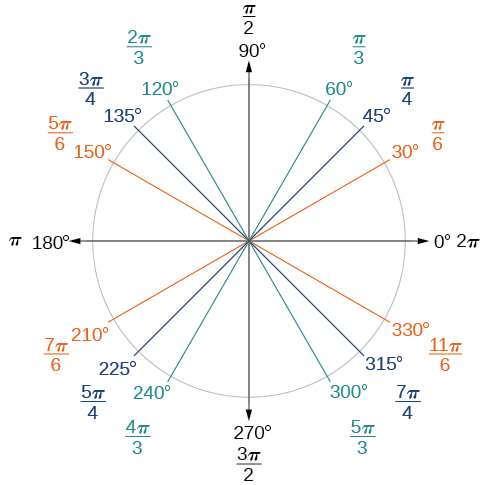
Now, we can list the corresponding radian values for the common measures of a circle corresponding to those listed in [link] , which are shown in [link] . Be sure you can verify each of these measures.
Find the radian measure of one-third of a full rotation.
For any circle, the arc length along such a rotation would be one-third of the circumference. We know that
So,
The radian measure would be the arc length divided by the radius.
Find the radian measure of three-fourths of a full rotation.
Because degrees and radians both measure angles, we need to be able to convert between them. We can easily do so using a proportion where is the measure of the angle in degrees and is the measure of the angle in radians.
This proportion shows that the measure of angle in degrees divided by 180 equals the measure of angle in radians divided by Or, phrased another way, degrees is to 180 as radians is to
To convert between degrees and radians, use the proportion
Convert each radian measure to degrees.
Because we are given radians and we want degrees, we should set up a proportion and solve it.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?