8.1 Graphs of the sine and cosine functions (Page 3/13)

Page 3 / 13

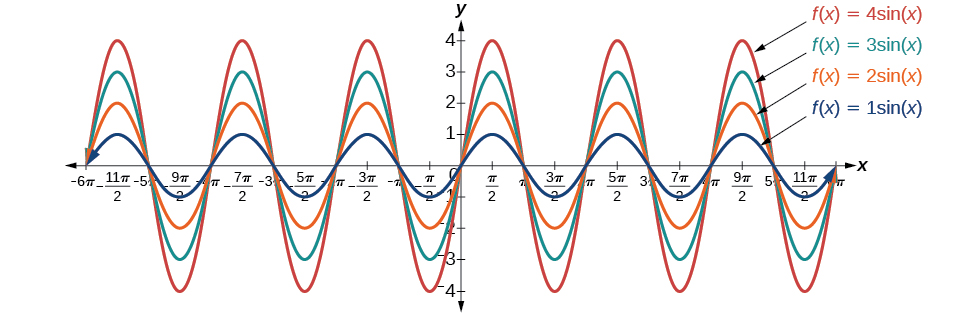
A graph with four items. The x-axis ranges from -6pi to 6pi. The y-axis ranges from -4 to 4. The first item is the graph of sin(x), which has an amplitude of 1. The second is a graph of 2sin(x), which has amplitude of 2. The third is a graph of 3sin(x), which has an amplitude of 3. The fourth is a graph of 4 sin(x) with an amplitude of 4.

A General Note Label

Amplitude of sinusoidal functions

If we let $C = 0$ and $D = 0$ in the general form equations of the sine and cosine functions, we obtain the forms

y = A \sin (B x) and y = A \cos (B x)

The amplitude is $A,$ and the vertical height from the midline is $| A | .$ In addition, notice in the example that

| A | = amplitude = \frac{1}{2} | maximum - minimum |

Identifying the amplitude of a sine or cosine function

What is the amplitude of the sinusoidal function $f (x) = −4 \sin (x) ?$ Is the function stretched or compressed vertically?

Let’s begin by comparing the function to the simplified form $y = A \sin (B x) .$

In the given function, $A = −4,$ so the amplitude is $| A | = | −4 | = 4.$ The function is stretched.

Got questions? Get instant answers now!

Try IT Feature

What is the amplitude of the sinusoidal function $f (x) = \frac{1}{2} \sin (x) ?$ Is the function stretched or compressed vertically?

$\frac{1}{2}$ compressed

Got questions? Get instant answers now!

Analyzing graphs of variations of y = sin x And y = cos x

Now that we understand how $A$ and $B$ relate to the general form equation for the sine and cosine functions, we will explore the variables $C$ and $D .$ Recall the general form:

\begin{matrix} y = A \sin (B x - C) + D and y = A \cos (B x - C) + D \\ o r \\ y = A \sin (B (x - \frac{C}{B})) + D and y = A \cos (B (x - \frac{C}{B})) + D \end{matrix}

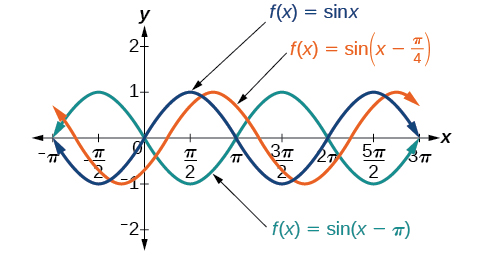
The value $\frac{C}{B}$ for a sinusoidal function is called the phase shift , or the horizontal displacement of the basic sine or cosine function . If $C > 0,$ the graph shifts to the right. If $C < 0,$ the graph shifts to the left. The greater the value of $| C |,$ the more the graph is shifted. [link] shows that the graph of $f (x) = \sin (x - π)$ shifts to the right by $π$ units, which is more than we see in the graph of $f (x) = \sin (x - \frac{π}{4}),$ which shifts to the right by $\frac{π}{4}$ units.

A graph with three items. The first item is a graph of sin(x). The second item is a graph of sin(x-pi/4), which is the same as sin(x) except shifted to the right by pi/4. The third item is a graph of sin(x-pi), which is the same as sin(x) except shifted to the right by pi.

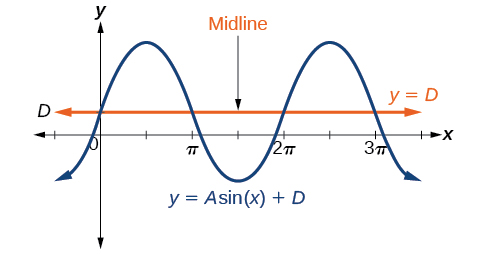
While $C$ relates to the horizontal shift, $D$ indicates the vertical shift from the midline in the general formula for a sinusoidal function. See [link] . The function $y = \cos (x) + D$ has its midline at $y = D .$

A graph of y=Asin(x)+D. Graph shows the midline of the function at y=D.

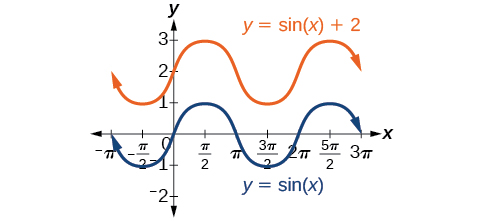
Any value of $D$ other than zero shifts the graph up or down. [link] compares $f (x) = \sin x$ with $f (x) = \sin x + 2,$ which is shifted 2 units up on a graph.

A graph with two items. The first item is a graph of sin(x). The second item is a graph of sin(x)+2, which is the same as sin(x) except shifted up by 2.

A General Note label

Variations of sine and cosine functions

Given an equation in the form $f (x) = A \sin (B x - C) + D$ or $f (x) = A \cos (B x - C) + D,$ $\frac{C}{B}$ is the phase shift and $D$ is the vertical shift .

Identifying the phase shift of a function

Determine the direction and magnitude of the phase shift for $f (x) = \sin (x + \frac{π}{6}) - 2.$

Let’s begin by comparing the equation to the general form $y = A \sin (B x - C) + D .$

In the given equation, notice that $B = 1$ and $C = - \frac{π}{6} .$ So the phase shift is

\begin{array}{r} \frac{C}{B} = - \frac{\frac{π}{6}}{1} \\ = - \frac{π}{6} \end{array}

or $\frac{π}{6}$ units to the left.

Got questions? Get instant answers now!

Try IT Feature

Determine the direction and magnitude of the phase shift for $f (x) = 3 \cos (x - \frac{π}{2}) .$

$\frac{π}{2};$ right

Got questions? Get instant answers now!

Identifying the vertical shift of a function

Determine the direction and magnitude of the vertical shift for $f (x) = \cos (x) - 3.$

Let’s begin by comparing the equation to the general form $y = A \cos (B x - C) + D .$

In the given equation, $D = −3$ so the shift is 3 units downward.

Got questions? Get instant answers now!

Try IT Feature

Determine the direction and magnitude of the vertical shift for $f (x) = 3 \sin (x) + 2.$

2 units up

Got questions? Get instant answers now!

How to Feature

Given a sinusoidal function in the form $f (x) = A \sin (B x - C) + D,$ identify the midline, amplitude, period, and phase shift.

Determine the amplitude as $| A | .$
Determine the period as $P = \frac{2 π}{| B |} .$
Determine the phase shift as $\frac{C}{B} .$
Determine the midline as $y = D .$

Questions & Answers

explain the basic method of power of power rule under indices.

Sumo Reply

Why is b in the answer

Dahsolar Reply

how do you work it out?

Brad Reply

answer

Ernest

heheheehe

Nitin

(Pcos∅+qsin∅)/(pcos∅-psin∅)

John Reply

how to do that?

Rosemary Reply

what is it about?

Amoah

how to answer the activity

Chabelita Reply

how to solve the activity

Chabelita

solve for X,,4^X-6(2^)-16=0

Alieu Reply

x4xminus 2

Lominate

sobhan Singh jina uniwarcity tignomatry ka long answers tile questions

harish Reply

t he silly nut company makes two mixtures of nuts: mixture a and mixture b. a pound of mixture a contains 12 oz of peanuts, 3 oz of almonds and 1 oz of cashews and sells for $4. a pound of mixture b contains 12 oz of peanuts, 2 oz of almonds and 2 oz of cashews and sells for $5. the company has 1080

ZAHRO Reply

If  , , are the roots of the equation 3 2 0, x px qx r     Find the value of 1  .

Swetha Reply

Parts of a pole were painted red, blue and yellow. 3/5 of the pole was red and 7/8 was painted blue. What part was painted yellow?

Patrick Reply

Parts of the pole was painted red, blue and yellow. 3 /5 of the pole was red and 7 /8 was painted blue. What part was painted yellow?

Patrick

how I can simplify algebraic expressions

Katleho Reply

Lairene and Mae are joking that their combined ages equal Sam’s age. If Lairene is twice Mae’s age and Sam is 69 yrs old, what are Lairene’s and Mae’s ages?

Mary Reply

23yrs

Yeboah

lairenea's age is 23yrs

ACKA

Katleho

Ello everyone

Katleho

Laurene is 46 yrs and Mae is 23 is

Solomon

hey people

christopher

age does not matter

christopher

solve for X, 4^x-6(2*)-16=0

Alieu

prove`x^3-3x-2cosA=0 (-π<A<=π

Mayank Reply

create a lesson plan about this lesson

Rose Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 5

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask

	6 Graphing variations of y = sin x And y = cos x By OpenStax Read Online Course
	4 Determining amplitude By OpenStax Read Online Course
©flickr: BK	Self Confidence By Miranda Reising Start Quiz
	1 Human A&P 2- Test 1 By Madison Christian Start Flashcards
	1 Microbiology Final 1 By Madison Christian Start Quiz
	1 AP Key Terms 01 Human Body Anatomy Physiology By OpenStax Start Key Terms
	5 Unified Modeling Language By JavaChamp Team Start Quiz
	Microbiology Practice Test By Sandhills MLT Start Test
	20 Sociology 20 Population Urbanization Environment By OpenStax Start Quiz
	1 Neuroscience Exam 2004 1 By David Corey Start Exam
	2 Understanding Societies 2 By Jessica Collett Start Exam
	10 Clin Sci I - GI Twedt quiz By Brooke Delaney Start Quiz