1. Home
  2. Algebra and trigonometry
  3. Trigonometric identities and
  4. Sum-to-product and product-to

9.4 Sum-to-product and product-to-sum formulas

<< Chapter < Page
  Algebra and trigonometry     Page 1 / 6
Chapter >> Page >
In this section, you will:
  • Express products as sums.
  • Express sums as products.
Photo of the UCLA marching band.
The UCLA marching band (credit: Eric Chan, Flickr).

A band marches down the field creating an amazing sound that bolsters the crowd. That sound travels as a wave that can be interpreted using trigonometric functions. For example, [link] represents a sound wave for the musical note A. In this section, we will investigate trigonometric identities that are the foundation of everyday phenomena such as sound waves.

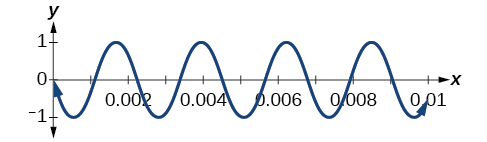
Graph of a sound wave for the musical note A - it is a periodic function much like sin and cos - from 0 to .01

Expressing products as sums

We have already learned a number of formulas useful for expanding or simplifying trigonometric expressions, but sometimes we may need to express the product of cosine and sine as a sum. We can use the product-to-sum formulas , which express products of trigonometric functions as sums. Let’s investigate the cosine identity first and then the sine identity.

Expressing products as sums for cosine

We can derive the product-to-sum formula from the sum and difference identities for cosine . If we add the two equations, we get:

cos   α   cos   β + sin   α   sin   β = cos ( α − β ) +     cos   α   cos   β − sin   α   sin   β = cos ( α + β ) ___________________________________ 2   cos   α   cos   β = cos ( α − β ) + cos ( α + β )

Then, we divide by   2   to isolate the product of cosines:

cos   α   cos   β = 1 2 [ cos ( α − β ) + cos ( α + β ) ]

Given a product of cosines, express as a sum.

  1. Write the formula for the product of cosines.
  2. Substitute the given angles into the formula.
  3. Simplify.

Writing the product as a sum using the product-to-sum formula for cosine

Write the following product of cosines as a sum:   2   cos ( 7 x 2 )   cos   3 x 2 .

We begin by writing the formula for the product of cosines:

cos   α   cos   β = 1 2 [ cos ( α − β ) + cos ( α + β ) ]

We can then substitute the given angles into the formula and simplify.

2   cos ( 7 x 2 ) cos ( 3 x 2 ) = ( 2 ) ( 1 2 ) [ cos ( 7 x 2 − 3 x 2 ) ) + cos ( 7 x 2 + 3 x 2 ) ] = [ cos ( 4 x 2 ) + cos ( 10 x 2 ) ] = cos   2 x + cos   5 x
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Use the product-to-sum formula to write the product as a sum or difference:   cos ( 2 θ ) cos ( 4 θ ) .

1 2 ( cos 6 θ + cos 2 θ )

Got questions? Get instant answers now!

Expressing the product of sine and cosine as a sum

Next, we will derive the product-to-sum formula for sine and cosine from the sum and difference formulas for sine . If we add the sum and difference identities, we get:

  sin ( α + β ) = sin   α   cos   β + cos   α   sin   β + sin ( α − β ) = sin   α   cos   β − cos   α   sin   β _________________________________________ sin ( α + β ) + sin ( α − β ) = 2   sin   α   cos   β

Then, we divide by 2 to isolate the product of cosine and sine:

sin   α   cos   β = 1 2 [ sin ( α + β ) + sin ( α − β ) ]

Writing the product as a sum containing only sine or cosine

Express the following product as a sum containing only sine or cosine and no products:   sin ( 4 θ ) cos ( 2 θ ) .

Write the formula for the product of sine and cosine. Then substitute the given values into the formula and simplify.

sin   α   cos   β = 1 2 [ sin ( α + β ) + sin ( α − β ) ] sin ( 4 θ ) cos ( 2 θ ) = 1 2 [ sin ( 4 θ + 2 θ ) + sin ( 4 θ − 2 θ ) ] = 1 2 [ sin ( 6 θ ) + sin ( 2 θ ) ]
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Use the product-to-sum formula to write the product as a sum:   sin ( x + y ) cos ( x − y ) .

1 2 ( sin 2 x + sin 2 y )

Got questions? Get instant answers now!

Expressing products of sines in terms of cosine

Expressing the product of sines in terms of cosine is also derived from the sum and difference identities for cosine. In this case, we will first subtract the two cosine formulas:

Questions & Answers

what is defense mechanism
Chinaza Reply
what is defense mechanisms
Chinaza
I'm interested in biological psychology and cognitive psychology
Tanya Reply
what does preconceived mean
sammie Reply
physiological Psychology
Nwosu Reply
How can I develope my cognitive domain
Amanyire Reply
why is communication effective
Dakolo Reply
Communication is effective because it allows individuals to share ideas, thoughts, and information with others.
effective communication can lead to improved outcomes in various settings, including personal relationships, business environments, and educational settings. By communicating effectively, individuals can negotiate effectively, solve problems collaboratively, and work towards common goals.
it starts up serve and return practice/assessments.it helps find voice talking therapy also assessments through relaxed conversation.
miss
Every time someone flushes a toilet in the apartment building, the person begins to jumb back automatically after hearing the flush, before the water temperature changes. Identify the types of learning, if it is classical conditioning identify the NS, UCS, CS and CR. If it is operant conditioning, identify the type of consequence positive reinforcement, negative reinforcement or punishment
Wekolamo Reply
please i need answer
Wekolamo
because it helps many people around the world to understand how to interact with other people and understand them well, for example at work (job).
Manix Reply
Agreed 👍 There are many parts of our brains and behaviors, we really need to get to know. Blessings for everyone and happy Sunday!
ARC
A child is a member of community not society elucidate ?
JESSY Reply
Isn't practices worldwide, be it psychology, be it science. isn't much just a false belief of control over something the mind cannot truly comprehend?
Simon Reply
compare and contrast skinner's perspective on personality development on freud
namakula Reply
Skinner skipped the whole unconscious phenomenon and rather emphasized on classical conditioning
war
explain how nature and nurture affect the development and later the productivity of an individual.
Amesalu Reply
nature is an hereditary factor while nurture is an environmental factor which constitute an individual personality. so if an individual's parent has a deviant behavior and was also brought up in an deviant environment, observation of the behavior and the inborn trait we make the individual deviant.
Samuel
I am taking this course because I am hoping that I could somehow learn more about my chosen field of interest and due to the fact that being a PsyD really ignites my passion as an individual the more I hope to learn about developing and literally explore the complexity of my critical thinking skills
Zyryn Reply
good👍
Jonathan
and having a good philosophy of the world is like a sandwich and a peanut butter 👍
Jonathan
generally amnesi how long yrs memory loss
Kelu Reply
interpersonal relationships
Abdulfatai Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask