| << Chapter < Page | Chapter >> Page > |
For any right triangle , given one other angle and the length of one side, we can figure out what the other angles and sides are. But what if we are given only two sides of a right triangle? We need a procedure that leads us from a ratio of sides to an angle. This is where the notion of an inverse to a trigonometric function comes into play. In this section, we will explore the inverse trigonometric functions .
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in [link] .

For example, if then we would write Be aware that does not mean The following examples illustrate the inverse trigonometric functions:
In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function , if then an inverse function would satisfy
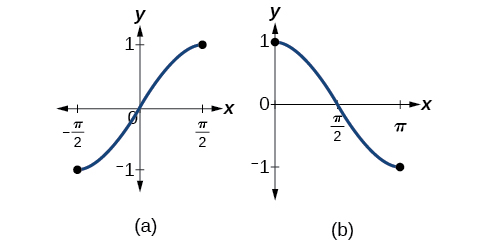
Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. [link] shows the graph of the sine function limited to and the graph of the cosine function limited to
[link] shows the graph of the tangent function limited to
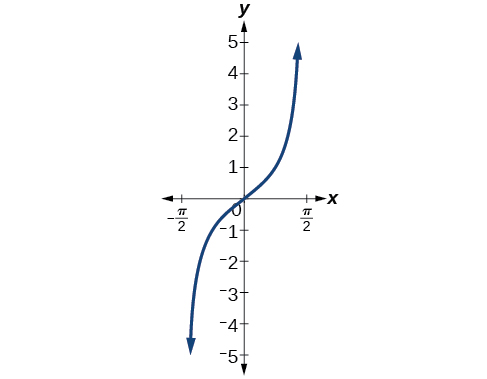
These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?