| << Chapter < Page | Chapter >> Page > |
General form of a confidence interval
(lower value, upper value) = (point estimate−error bound, point estimate + error bound)
To find the error bound when you know the confidence interval
error bound = upper value−point estimate OR error bound =
Single Population Mean, Known Standard Deviation, Normal Distribution
Use the Normal Distribution for Means, Population Standard Deviation is Known EBM = z
The confidence interval has the format ( − EBM , + EBM ).
Use the following information to answer the next five exercises: The standard deviation of the weights of elephants is known to be approximately 15 pounds. We wish to construct a 95% confidence interval for the mean weight of newborn elephant calves. Fifty newborn elephants are weighed. The sample mean is 244 pounds. The sample standard deviation is 11 pounds.
Identify the following:
In words, define the random variables X and .
Construct a 95% confidence interval for the population mean weight of newborn elephants. State the confidence interval, sketch the graph, and calculate the error bound.
What will happen to the confidence interval obtained, if 500 newborn elephants are weighed instead of 50? Why?
As the sample size increases, there will be less variability in the mean, so the interval size decreases.
Use the following information to answer the next seven exercises: The U.S. Census Bureau conducts a study to determine the time needed to complete the short form. The Bureau surveys 200 people. The sample mean is 8.2 minutes. There is a known standard deviation of 2.2 minutes. The population distribution is assumed to be normal.
Identify the following:
In words, define the random variables X and .
X is the time in minutes it takes to complete the U.S. Census short form. is the mean time it took a sample of 200 people to complete the U.S. Census short form.
Which distribution should you use for this problem?
Construct a 90% confidence interval for the population mean time to complete the forms. State the confidence interval, sketch the graph, and calculate the error bound.
CI: (7.9441, 8.4559)
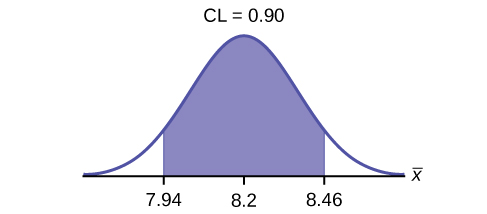
EBM = 0.26
If the Census wants to increase its level of confidence and keep the error bound the same by taking another survey, what changes should it make?
If the Census did another survey, kept the error bound the same, and surveyed only 50 people instead of 200, what would happen to the level of confidence? Why?
The level of confidence would decrease because decreasing n makes the confidence interval wider, so at the same error bound, the confidence level decreases.
Suppose the Census needed to be 98% confident of the population mean length of time. Would the Census have to survey more people? Why or why not?
Use the following information to answer the next ten exercises: A sample of 20 heads of lettuce was selected. Assume that the population distribution of head weight is normal. The weight of each head of lettuce was then recorded. The mean weight was 2.2 pounds with a standard deviation of 0.1 pounds. The population standard deviation is known to be 0.2 pounds.

Notification Switch
Would you like to follow the 'Introductory statistics' conversation and receive update notifications?